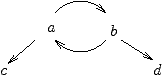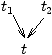Chapitre 2 Définitions préliminaires
2.1 Introduction
Le but de ce chapitre est de donner un certain nombre de définitions
et de résultats classiques. Le lecteur familier avec les notions de
base de la réécriture (algèbre de termes, système de réécriture,
confluence, normalisation forte, λ-calcul, typage…) peut
passer ce chapitre.
Nous commencerons par rappeler les définitions de base concernant les
relations binaires sur un ensemble. Nous donnerons alors des
définitions formelles de normalisation et de confluence
pour une relation ainsi que quelques résultats concernant ces notions.
Nous définirons ensuite les notions d'algèbre de termes, de
règle et de système de réécriture du premier ordre et
nous présenterons quelques résultats simples ayant trait à la
confluence et à la normalisation des systèmes de réécriture du premier
ordre. Nous conclurons ce chapitre par une présentation rapide du
λ-calcul [Chu41] et d'une extension du λ-calcul
possédant un mécanisme explicite de gestion des
substitutions [BR95].
2.2 Rappels sur la notion de relation binaire
Définition 1
Soit E un ensemble:
-
Une relation binaire R sur E est un sous ensemble
de E× E. Si (e1,e2)∈ R, nous dirons que e1 est
en relation avec e2 (par R) (l'inverse n'étant pas
forcément vrai). Nous utiliserons désormais la notation
e1 R e2 pour exprimer le fait que l'élément e1 est en
relation avec e2.
- Une relation réflexive est une relation binaire R sur
E telle que tout élément de E est en relation avec lui-même.
- Une relation antiréflexive est une relation binaire
R sur E telle qu'aucun élément de E n'est en relation avec
lui-même.
- Une relation symétrique est une relation binaire R
sur E telle que pour tout couple d'éléments e1 et e2 de E,
si e1 R e2 alors e2 R e1.
- Une relation R est antisymétrique si pour tout
couple d'éléments e1,e2 de E: si e1 R e2 et si
e2 R e1 alors e1 = e2.
- Une relation R est transitive si pour tous
d'éléments e1 ,e2 et e3 tels que e1 R e2 et si
e2 R e3 alors e1 R e3.
- Une relation R est une relation d'équivalence
si R est symétrique, transitive et réflexive.
- Une relation R est un ordre si R
est réflexive, transitive et antisymétrique.
- R est un ordre strict si R
est antiréflexive (donc antisymétrique) et transitive.
- Un ordre (strict) > est dit
nœthérien s'il n'existe pas
de suite infinie (ti)i∈N telle que pour tout
i∈N, ti > ti+1.
Si nous considérons l'ensemble des entiers naturels N:
l'égalité est une relation d'équivalence sur cet ensemble alors que la
relation d'ordre usuelle > est un ordre strict au sens de la
définition précédente. Cet ordre est, de plus, nœthérien.
Définition 2 (Extensions d'une relation binaire)
Soient E un ensemble et → une relation binaire sur cet
ensemble.
-
La clôture transitive →+ de → est la
plus petite relation (pour l'inclusion) transitive contenant
→.
- La clôture réflexive et transitive →* de
→ est la plus petite relation réflexive et transitive
contenant →.
Si →1 et →2 sont deux relations binaires,
nous définissons leur union, notée →1 ∪
→2, comme étant la plus petite relation contenant à la fois
→1 et →2.
Définition 3 (Ordre lexicographique)
Soient E1 et E2 deux ensembles et >1 et >2 deux ordres
sur, respectivement, E1 et E2. Nous définissons
l'ordre lexicographique
>lex induit par >1 et >2 sur l'ensemble E1×
E2 comme suit:
| (e1,e2)>lex(e1',e2') ⇔ | ⎧
⎪
⎨
⎪
⎩ | | e1 | >1 | e1' | |
| ou |
| e1 | = | e1' | | et | | e2 | >2 | e2' |
|
|
Il est à remarquer que:
-
la relation >lex est bien un ordre (strict dès que >1 et >2
le sont).
- On peut étendre cette définition à un nombre fini quelconque
d'ensembles munis d'ordres.
2.3 Terminaison et confluence
Définition 4 (Réduit d'un terme et formes normales)
Soient E un ensemble et → une relation binaire sur E.
Lemme 5 (Relation entre les différentes notions de normalisabilité)
Soit E un ensemble.
-
Si → est une relation sur E, alors tout élément de
E fortement normalisable par → est faiblement
normalisable par →.
- Toute relation → fortement normalisante sur E est
faiblement normalisante sur E.
Remarque 6
Soient E un ensemble et → une relation binaire sur cet
ensemble. La relation → est fortement normalisante sur E
si et seulement si la relation →+ est fortement
normalisante sur E.
Lemme 7
Soient E un ensemble et → une relation binaire sur E.
La relation → est fortement normalisante sur E si et
seulement s'il existe un ordre nœthérien strict > tel que:
e→ e ' implique e>e '.
Nous utiliserons le lemme suivant pour prouver la terminaison de
certains systèmes de réécriture.
Lemme 8
Soit O un ensemble. Soient R1 et R2 deux relations sur
O telles que:
-
R2 est fortement normalisante,
- Il existe un ensemble O', une relations R' sur cet
ensemble et une fonction T de O dans O'
tels que:
-
a→R1 b implique T(a)—→R'+ T(b)
- a→R2 b implique T(a)= T(b)
Pour tout terme a∈ O tel que T(a) est
R'-fortement normalisable, a est (R1∪ R2)-fortement
normalisable.
-
- Preuve.
Par contradiction [FKP99].
Les propriétés de normalisation (faible ou forte) garantissent
l'existence d'une "valeur" pour les éléments de E mais pas l'unicité
de cette valeur. L'unicité (en cas d'existence) est assurée par la
notion de confluence décrite ci-dessous.
Définition 9 (Confluence)
Soient E un ensemble et → une relation binaire sur E.
-
La relation → est dite
confluente si:
| ∀ e, e1, e2, |
| |
| ⎫
⎬
⎭ | ⇒ ∃ e ', | ⎧
⎨
⎩ | |
|
- La relation → est dite localement confluente si:
| ∀ e, e1, e2, |
| |
| ⎫
⎬
⎭ | ⇒ ∃ e ', | ⎧
⎨
⎩ | |
|
- La relation → est dite fortement confluente ou possède
la propriété du diamant si:
| ∀ e, e1, e2, |
| |
| ⎫
⎬
⎭ | ⇒ ∃ e ', | ⎧
⎨
⎩ | |
|
Ces trois notions de confluence sont bien évidement liées.
Remarque 10
Toute relation confluente est localement confluente.
Lemme 11 (Newman)
Toute relation localement confluente
et fortement
normalisante
sur un ensemble est confluente
sur cet
ensemble.
Ce lemme est classique [New42]. Voir aussi le livre de Baader
et Nipkow [BN98].
Il est à remarquer que les deux conditions de ce lemme sont
nécessaires. En effet, il existe des relations localement
confluentes et non fortement normalisantes qui ne sont pas
confluentes et bien évidement toute relation non
localement confluente n'est pas confluente.
Nous ne donnerons ici qu'un exemple du premier cas. Considérons
la relation → définie sur
l'ensemble { a,b,c,d } et dont le
graphe est le suivant:
Cette relation est trivialement non fortement normalisante (bien que
faiblement normalisante), puisque par exemple a→ b→ a…
Elle est non confluente car, par exemple, a—→* c et a—→* d
bien que c et d ne possèdent pas de réduit en commun. Pourtant
cette relation est localement confluente.
Lemme 12
Toute relation fortement confluente
est confluente
.
Enfin nous concluons cette section par lemme suivant:
Lemme 13 (Lemme d'interprétation)
Soit R= R1∪ R2 l'union de deux relations.
Si:
-
R1 est confluente et fortement normalisante,
- il existe une relation R' sur les R1-formes
normales telle que:
-
R'⊂ R*,
- Pour toutes expressions e1 et e2:
| e1→ R2 e2 implique
R1(e1)—→* R' R1(e2) |
où R1(e) désigne l'unique forme normale pour
R1 de e.
alors R est confluente si et seulement si R' l'est.
-
- Preuve.
La preuve de ce lemme peut être trouvée
dans [CHL96].
2.4 Réécriture du premier ordre
2.4.1 Algèbre de termes
Définition 14 (Signature)
Une signature est un ensemble Σ muni
d'une fonction d'arité, notée ar( ), de Σ
dans N. Les éléments d'une signature seront par la suite
généralement notés f, g,… Notation 15
Dans la suite de ce document, nous nous autoriserons à partitionner
l'ensemble Σ en une union infinie d'ensembles
(Σi)i∈N où chaque Σi est l'image
réciproque de l'entier i par la fonction ar( ).
Définition 16 (Algèbre de termes du premier ordre)
Étant donné une signature Σ et un ensemble X de
variables, possiblement infini, nous définissons l'algèbre des termes A=T(Σ, X) comme
suit:
-
Toute variable x∈ X est un terme (un élément de
A).
- Si f est un élément de Σn et si t1,…,tn sont des
termes alors f(t1,…,tn) est un terme.
Cette notion d'algèbre de termes nous permettra de définir tous les
systèmes de réécriture du premier ordre. Pour les systèmes de
réécriture d'ordre supérieur nous aurons aussi besoin d'une
notion de lieur.
De très nombreux exemples d'algèbres de termes peuvent être donnés.
Exemple 17
-
Définissons la signature Σ1=({0,s},{ar(0)=0,
ar(s)=1}). L'algèbre A1=T(Σ1,∅) est une
représentation de l'ensemble des entiers naturels puisque tout
entier naturel peut être vu soit comme l'entier nul représenté par
0, soit comme le successeur d'un entier n représenté par
s(n) où n est la représentation de n.
- Définissons maintenant la signature Σ2 en ajoutant à
la signature Σ1 le symbole plus d'arité 2. L'algèbre
A2=T(Σ2,∅) est une représentation des
sommes d'entiers telles que:
plus(3,plus(7,4)).
Définition 18 (Variables d'un terme)
Étant donné une algèbre de termes A=T(Σ, X), et
un terme t de cette algèbre, nous définissons
l'ensemble des variables de t,
BV(t) par induction sur la structure de t comme suit:
-
Si t=x∈ X alors BV(t)={x}
- Si t=f(t1,…,tn) alors BV(t)=∪i=1n
BV(ti)
Nous aurons ainsi BV(plus(x,plus(s(y),0)))={x,y}.
Définition 19 (Termes clos)
Soit A une algèbre de termes. Nous appellerons
dans la suite terme clos tout terme t de cette
algèbre tel que BV(t)=∅.
Définition 20 (Position dans un terme)
Une position est une suite finie (un mot
)
d'entiers naturels strictement positifs. Nous noterons par la suite
une position i1.i2.… in quand la suite ne sera pas vide et
є la suite vide.Étant donné une algèbre de termes T(Σ, X), et un terme
t de cette algèbre, nous définissons l'ensemble des positions de t, Pos(t) par induction sur la
structure de t comme suit:
-
Si t=x∈ X, Pos(t)={є}.
- Si t=f∈Σ0, Pos(t)={є}.
- Si t=f(t1,…,tn) où n>0,
Pos(t)={є}∪∪i=1n(∪p∈Pos(ti)i.p).
Nous appellerons position propre toute
position autre que la position є.
Ainsi l'ensemble des positions de plus(s(0),s(s(y))) est
{є,1,2,1.1,2.1,2.1.1}
Les positions dans un terme nous permettent, de définir les notions de
sous-terme à une position donnée et de sous-terme d'un
terme.
Définition 21 (Sous-termes d'un terme)
Étant donné un terme t et une position p de ce terme, nous
définissons le sous-terme
de t à la position p, notée t∣p, par
induction sur p:
-
Si p=є, alors t∣є=t.
- Si p=i.p', alors t=f(t1,…,ti,…,tn) et
t∣p=ti∣p'.
Nous dirons qu'un terme t' est un sous-terme d'un terme t s'il existe une position p∈Pos(t)
telle que t'=t∣p.
Ainsi,
plus(s(0),s(s(y)))∣1.1=s(0)∣1=0∣є=0
et plus(s(0),s(s(y)))∣2=s(s(y)).
Définition 22 (Greffe d'un terme à une position)
Soient t et t' deux termes et p une position de t. Nous
définissons la greffe du terme t' à la
position p dans le terme t, noté
t[t']p par induction sur p comme suit:
-
Si p=є alors t[t']є =
t'.
- Si p=i.p' et t=f(t1,…,ti,…,tn) alors:
| t[t']i.p'=f(t1,…,ti[t]p',…,tn) |
2.4.2 Règles et systèmes de réécriture du premier ordre
Dans cette section, nous allons définir la notion de règle de
réécriture et de système de réécriture du premier ordre.
Définition 23 (Règles de réécriture)
Supposons donnée une algèbre de termes A=T(Σ,
X). Une règle de réécriture, notée
g → d, est la donnée de deux termes g et d appelés
respectivement membre gauche et
membre droit de la règle tels que:
-
g n'est pas une variable,
- BV(d)⊂ BV(g).
Ainsi, suivant cette définition, si on considère l'algèbre
représentant l'ensemble des expression entières:
-
plus(0,x)→ x est bien une règle de réécriture,
- x→ 0 n'est pas une règle de réécriture car x est une
variable,
- plus(0,0)→ x n'est pas une règle de réécriture car x
n'est pas une variable du terme plus(0,0).
Définition 24 (Système de réécriture)
Un système de réécriture sur une
algèbre de termes est la donnée d'un ensemble de règles de
réécriture de cette algèbre.
Avant de définir la notion de relation de réduction du premier
ordre engendrée par un système de réécriture il nous faut préciser
la notion de substitution du premier ordre (ou remplacement).
2.4.3 Remplacement du premier ordre
Cette section est consacrée à la définition de la notion de
remplacement de premier ordre. Un remplacement est une
fonction des variables d'une algèbre de termes dans les termes de
cette algèbre. Nous utiliserons de tels objets pour transformer les
termes.
Définition 25 (Remplacement)
Soit T(Σ, X) une algèbre de termes. Un
remplacement σ est une fonction de
X dans T(Σ, X) telle que pour toute variable x
de X, sauf un nombre fini d'entre elles, σ(x)=x.Nous appellerons par la suite domaine
d'un remplacement σ, noté dom(σ), l'ensemble des
variables x∈ X telles que σ(x)≠ x et
codomaine de ce remplacement, noté
codom(σ), l'ensemble
∪x∈dom(σ) BV(σ(x)).
Remarquons que nous pouvons aussi représenter les remplacements comme
étant des ensembles (finis) de couples (x,t) où x est une variable et t
un terme.
Définition 26 (Application d'un remplacement à un terme)
Étant donné un remplacement σ et un terme t, nous
définissons l'application de
σ à t, notée t σ, par induction sur la structure du
terme t comme suit:
-
xσ=σ(x) si x est une variable.
- f(t1,…,tn)σ=f(t1σ,…,tnσ).
Nous aurons donc par exemple plus(x,y)σ=plus(0,y) si
σ={(x,0)}.
Définition 27 (Renommage)
Un renommage est un remplacement ρ tel que
∀ x∈dom(ρ), ρ(x)∈ X.
Définition 28
Nous dirons par la suite que deux termes t1 et t2 sont
unifiables si et seulement s'il existe un
remplacement σ, appelé
unificateur de t1 et t2, tel
que t1σ=t2σ.
Définition 29
Étant donné deux remplacements ρ1 et ρ2, nous dirons que
ρ1 est plus
général que ρ2, ce que nous noterons dans la suite de ce
document ρ1>>ρ2, si et seulement s'il existe un
remplacement ρ3 tel que: ρ2=ρ3∘ρ1
Définition 30 (Unificateur le plus général de deux termes)
Nous appellerons un unificateur le plus général de deux termes
unifiables t1 et t2, un élément de l'ensemble des unificateurs
de t1 et t2 qui est minimal pour l'ordre >>.
2.4.4 Relation induite par un système de
réécriture
Nous allons, dans cette section, définir la relation (de
réduction) induite par un système de réécriture, pour cela nous
avons besoin de définir la notion de clôture par contexte d'une
relation binaire.
Définition 31 (Relation de réduction en tête)
Soient A= A(Σ, X) une algèbre de termes et R
un système de réécriture sur A. La relation de réduction en tête induite par R, notée
—→Rh , est définie comme suit.
Le terme e ' est un réduit du terme e par la relation —→Rh
si et seulement si:
-
Il existe une règle G→ D appartenant au système R,
- Il existe un remplacement de premier ordre σ,
- e=Gσ et e '=Dσ .
Exemple 32
Le terme 3 est un réduit en tête de plus(3,0) par le système de
réécriture {plus(n,0)→ n}. Il suffit de prendre
σ={n↦ 3}
Définition 33 (Contexte)
Un contexte C pour une algèbre
T(Σ,X) est un terme de l'algèbre
T(Σ∪{ },X) contenant exactement une
occurrence du symbole 0-aire (d'arité 0) ∉Σ.Étant donné un contexte C et un terme t∈
T(Σ,X), la notation C(t) désigne le terme
Cσ de l'algèbre T(Σ,X) où
σ={(,t)}.
Ainsi si nous considérons le contexte C=plus(,0) alors
C(3)=plus(3,0).
Définition 34 (Clôture par contexte d'une relation)
Soient A= A(Σ, X) une algèbre de termes et R
une relation binaire sur A.La relation R est dite close
par contexte pour A si:
Pour tout symbole de fonction n-aire f de Σ, pour
tous termes t1,…,tn, s'il existe un i∈[1… n] et
un terme ti' tel que ti R ti' alors:
| f(t1,…,ti,…,tn) R f(t1,…,ti',…,tn) |
ou, de manière équivalente, pour tout contexte C et pour
tous termes t R t', C(t) R C(t').
La clôture par contexte d'une
relation R est la plus petite relation R' contenant R et close
par contexte.
Remarque 35
Un terme t1 est un sous-terme d'un terme t2 si et seulement si
il existe un contexte C tel que t2=C(t1).
Il nous est maintenant possible de définir la notion de relation
(de réduction) induite par un système de réécriture.
Définition 36 (Relation de réduction)
Soient A= A(Σ, X) une algèbre de termes et R
un système de réécriture sur A. La relation de réduction induite par R, notée →R ,
est définie comme étant la clôture par contexte de la relation
—→Rh .
Ainsi, le terme plus(0,3) est un réduit du terme plus(0,plus(3,0))
par la relation induite par le système de réécriture { plus(n,0)→
n}.
Définition 37
Soient l1→ r1 et l2→ r2 deux règles d'un système de
réécriture R telles que l1 soit unifiable avec un sous-terme de
l2 qui ne soit pas une variable (ce sous-terme doit être propre
si l1→ r1 = l2→ r2).Dans ce cas, il existe un contexte C, un terme u et un
unificateur plus général σ de u et l1 tels que
l2=C(u). Nous appellerons alors le couple de terme
(C(r1)σ,r2σ) une paire
critique du système R.
Une paire critique (t1,t2) est dite joignable s'il existe un
terme t tel que:
Ainsi, le système:
| R= | ⎧
⎪
⎨
⎪
⎩ | | f(f(x,y),z) | → | f(x,f(y,z)) |
| f(i(t),t) | → | e |
| | → |
|
|
possède une paire critique obtenue en applicant l'unificateur le plus
général ρ={ x↦ i(t), y↦ t } à ses deux règles.
Cette paire est: (f(i(t),f(t,z)) , f(e,z) )
La notion de paire critique est très importante vis à vis de celle de
confluence. En effet:
Lemme 38 (Paires critiques du premier ordre et confluence locale [BN98])
Soit R un système de réécriture du premier ordre. Si toutes les
paires critiques sont joignables alors le système R est localement
confluent.
Concluons ce rapide aperçu de la notion de réécriture du premier ordre
et d'algèbre de terme par la définition de congruence.
Définition 39 (Congruence)
Supposons donnée une algèbre de termes A=T(Σ, X).
Une congruence (sur A) est une relation
d'équivalence ≡ telle que:
| t1≡ t1', … tn≡ tn' ⇒
f(t1,…,tn)≡ f(t1',…,tn')
|
Définition 40 (Réécriture modulo)
Supposons données une algèbre de termes A=T(Σ,
X), ≡ une congruence et → une relation de réécriture.
Nous dirons qu'un terme t1 se réécrit par la relation →
quotientée par la congruence ≡ en un terme t2 si et
seulement si:
| ∃ t1', ∃ t2', t1≡ t1' → t2'≡ t2
|
2.5 Le λ-calcul
Les algèbres de termes du premier ordre,
(définition 16), et les systèmes de réécriture
du premier ordre ne permettent pas de modéliser les fonctions
d'ordre supérieur (telles que, par exemple, la fonction map).
Ces fonctions ne peuvent être modélisées que dans le cadre des
formalismes de réécriture d'ordre supérieur.
Comme nous l'avons déjà mentionné dans l'introduction de ce document,
le λ-calcul [Chu41] est le plus ancien et, sans doute, le
mieux connu des systèmes de réécriture d'ordre supérieur. Les
formalismes présentés dans la suite de ce document n'en sont que des extensions.
Nous présenterons, dans cette section, le λ-calcul avant de
rappeler que ce formalisme n'est pas fortement normalisant. Nous
présenterons alors un système de types simples permettant de
retrouver la terminaison ainsi que de garantir la cohérence des
données. Nous conclurons cette section par la présentation d'une
extension très simple de ce calcul à la gestion explicite du mécanisme
de substitution.
2.5.1 Le λ-calcul non typé
Nous nous donnons un ensemble infini dénombrable X de
variables.
L'ensemble des λ-termes est donné par la
grammaire suivante.
| (Termes) t | ::= | x | (Variable) |
| | ∣ | t t | (Application) |
| | ∣ | λ x. t | (Abstraction) |
| où x∈ X
|
Intuitivement, le λ-terme λ x. t représente une fonction
qui associe la valeur t à la variable x. Le terme
f t représente l'application de la fonction f à un argument
t.
Comme en mathématiques, la variable x de la construction
λ x. t est une variable muette (ou liée) au sens où,
par exemple, les deux termes λ x. x et λ y. y
représentent la même fonction. Ces deux termes seront dit
α-équivalents. Nous allons maintenant donner une formalisation
de cette notion. Pour cela il nous faut introduire la notion
d'ensemble des variables libres d'un λ-terme.
Définition 41 (Variables Libres)
L'ensemble des variables
libres d'un λ-terme t, noté FV(t), est
défini par induction sur la structure de t comme suit:
| FV(x) | = | {x} |
| FV( t1 t2) | = | FV(t1)∪ FV(t2) |
| FV(λ x. t1) | = | FV(t1)∖{x} |
Ainsi, nous avons:
| FV(λ x. x) | = | ∅ |
| FV(λ x. y) | = | {y} |
| FV( (λ x. y) z) | = | {y,z} |
Définition 42 (Variables liées)
L'ensemble des variables
liées d'un λ-terme t, noté BV(t), est défini
par induction sur la structure de t comme suit:
| BV(x) | = | ∅ |
| BV( t1 t2) | = | BV(t1)∪ BV(t2) |
| BV(λ x. t1) | = | {x}∪ BV(t1) |
Ainsi, nous avons:
| BV(λ x. x) | = | {x} |
| BV(λ x. y) | = | {x} |
| BV( (λ x. y) z) | = | {x} |
Définition 43 (Application d'un remplacement à un λ-terme)
Un remplacement σ
dans le λ-calcul est un remplacement tel que défini pour le
premier ordre (Définition 25)
mais à valeur dans l'ensemble des λ-termes.L'application d'un remplacement
ρ={(x1,t1),…,(xn,tn)} à un λ-terme est défini
comme suit:
| xσ | =def | σ(x) | |
| ( t1 t2)σ | =def | t1σ t2σ |
| (λ xi. t)ρ | =def | λ xi. (tρ'i) | où ρ'i={(xj,tj)}j∈{1,…,i−1,i+1,…,n} |
| (λ y. t)ρ | =def | λ y. (tρ) | où y∉{x1,…,xn} |
Nous sommes désormais en mesure de définir formellement la notion de
termes α-équivalents.
Définition 44 (α-équivalence)
Deux termes t1 et t2 sont dit α-équivalents, ce
que nous noterons par la suite t1=α t2, si et seulement si:
-
Ou bien t1=t2=x
- Ou bien t1=( t11 t12),
t2=( t21 t22), t11=α t21 et t12=α
t22,
- Ou bien t1=λ x1. t1', t2=λ x2. t2' et
pour tous renommages ρ1={(x1,z)} et ρ2={(x2,z)},
sauf un nombre fini, t1'ρ1=α t2'ρ2.
Nous travaillerons désormais tout au long de cette section modulo
α-équivalence.
Définition 45 (Substitution)
Une substitution σ est un couple { x ← t } formé
d'une variable x et d'un λ-terme t.
Étant donné un λ-terme t et une substitution
σ={ x ← t' } , nous définissons l'application de
σ au terme t par induction sur t comme suit:
| x | { x ← t' } =def | t' |
| y | { x ← t' } =def | y | si y≠ x |
| ( t1 t2) | { x ← t' } =def | ( t1{ x ← t' } t2{ x ← t' } ) |
| (λ y. t1) | { x ← t' } =def | λ y. (t1{ x ← t' } ) | si
x≠ y et y∉ FV(t') |
Remarquons que la condition sur l'abstraction n'est pas
restrictive puisque si y∈{x}∪ FV(t'), il nous suffit de
remplacer λ y. t1 par un terme λ z. t1' qui lui
soit α-équivalent et tel que z∉{x}∪ FV(t).
Nous pouvons également remarquer que l'application d'une substitution à un
λ-terme n'est pas défini à l'aide de règles du λ-calcul
mais en dehors de ce calcul (de manière implicite).
Grâce à la notion de substitution du λ-calcul, nous pouvons
désormais définir l'unique règle de réduction du λ-calcul:
| (β-règle) (λ x. t) t'→β
t{ x ← t' }
|
Notation 46
Nous noterons →λ (ou, quand la confusion ne sera pas
possible, → ) la clôture par contexte de la
β-règle:
Le formalisme du λ-calcul est confluent sur l'ensemble de ses
termes:
Lemme 47 (Confluence du λ-calcul [Bar84])
Le système de réécriture induit par la β-règle est confluent.
Cependant, le λ-calcul ne possède pas la propriété de normalisation
forte comme le prouve l'exemple suivant:
Exemple 48 (Contre exemple de terminaison du λ-calcul)
Le terme Ω Ω où
Ω=defλ x. ( x x) n'est pas fortement
normalisant. En effet, nous avons la séquence de réduction infinie
suivante:
| Ω Ω | =def | λ x. ( x x) Ω |
| | → | ( x x){ x ← Ω } |
| | = | Ω Ω |
| | ⋮ |
De plus la trop grande puissance du λ-calcul nous ôte tout espoir:
Lemme 49 (Indécidabilité de la terminaison)
Il n'est pas possible de décider de la normalisation forte
des λ-termes.
-
- Preuve.
[Bar84]
Il est donc nécessaire de donner un critère syntaxique de
normalisation forte pour les λ-termes. Ce critère devra bien
évidement être correct (tout λ-terme le vérifiant devant être
fortement normalisable) mais ne pourra être complet (il
existera des λ-termes fortement normalisables qui ne vérifierons
pas ce critère).
L'un des critères les plus connus est sans doute le "bon typage" dans
un système de types simples.
2.5.2 Le système de types simples
De nombreux systèmes de types ont été proposés pour le λ-calcul [Bar93].
Nous présenterons ici le plus simple d'entre eux.
Définition 50 (Types simples)
L'ensemble des types simples du
λ-calcul [Bar84] est défini par la grammaire
suivante:
| (Types) A | ::= | ι | (Type primitif) |
| | ∣ | A→A | (Type fonctionnel) |
Intuitivement, le type ι représente les types de bases
(entiers,réels, (chaînes de) caractères …) alors que les types
fonctionnels représentent les types des fonctions.
Le type int→bool est le type des fonctions des entiers dans les
booléens (par exemple celui de la fonction est_paire).
Nous utiliserons désormais les notations A, B, C …pour
désigner des types simples.
Définition 51 (λ-termes annotés)
L'ensemble des λ-termes annotés est donné par la même
grammaire que l'ensemble des λ-termes mais où nous avons remplacé
la construction λ x. t du λ-calcul par λ x :
A. t où A est un type.
Définition 52 (Environnement de types)
Un environnement de types, Γ, est un ensemble de couples
x : A, où x est une variable et A est un type simple, tel
que toute variable x apparaît au plus une fois dans Γ.
Définition 53 (Jugement de typage)
Un jugement de typage est un triplet Γ⊢ t : A
où Γ est un environnement de types, t est un λ-terme annoté
et A est un type.Nous dirons que le λ-terme annoté t possède le type A dans
l'environnement Γ s'il est possible de dériver le jugement
Γ⊢ t : A en appliquant l'ensemble de règles suivant:
|
(Var) | si (x,A)∈Γ |
| |
| x : A,Γ⊢ t : B |
|
| Γ⊢λ x :
A. t :
A→B |
(Abs) |
| |
| Γ⊢ t1 : A→B Γ⊢ t2 :
A |
|
| Γ⊢ ( t1 t2) : B |
(App) |
Notation 54
Dans la suite, nous utiliserons la notation
Γ⊢ t : A pour exprimer que t possède le type A dans
l'environnement Γ.
Nous aurons ainsi n : ι⊢
(λ x : ι. x) n : ι par la dérivation
suivante:
|
(Var) |
|
| n : ι⊢
λ x : ι. x : ι→ι |
(Abs)
(Var) |
|
| n : ι⊢
(λ x : ι. x) n : ι |
(App) |
Théorème 55 (Préservation de types par réduction [Bar93])
Soient t et t' deux λ-termes, Γ un environnement de
types et A un type. Si Γ⊢ t : A et t→ t'
alors Γ⊢ t' : A.
Théorème 56 (Normalisation forte du λ-calcul simplement typé [Bar93])
Soient t un λ-terme, Γ un environnement de types et A
un type. Si Γ⊢ t : A alors t est fortement
normalisable.
2.5.3 Extensions aux systèmes de substitutions explicites
Nous présentons ici la plus simple des extensions du λ-calcul
permettant la gestion explicite de la substitution: le
λx-calcul [BR95, BG99]. L'idée principale de ce
calcul est d'enrichir la syntaxe du λ-calcul d'un constructeur de
substitution explicite en remplaçant la méta--notation
t{ x ← t' } par la construction syntaxique t [ x/t' ] et de
transposer les méta--règles de substitutions du λ-calcul en des
règles explicites du λx-calcul.
Définition 57 (Grammaire du λx-calcul)
Les termes du λx-calcul sont donnés par la grammaire suivante:| (Termes) t | ::= | x | (Variable) | où x∈ X. |
| | ∣ | t t | (Application) |
| | ∣ | λ x. t | (Abstraction) |
| | ∣ | t [ x/t ] | (Substitution Explicite) |
Remarquons que les termes du λ-calcul sont en particulier des
termes du λx-calcul.
Définition 58 (Variables libres et liées d'un terme du λx-calcul)
Soit t un terme du λx calcul. L'ensemble des
variables
libres de t est défini par induction sur t comme suit:
| FV(x) | = | {x} |
| FV( t1 t2) | = | FV(t1)∪ FV(t2) |
| FV(λ x. t1) | = | FV(t1)∖{x} |
| FV( t [ x/t' ] ) | = | ( FV(t)∖{x})∪ FV(t') |
L'ensemble des variables liées de t est défini par
induction sur t comme suit:
| BV(x) | = | ∅ |
| BV( t1 t2) | = | BV(t1)∪ BV(t2) |
| BV(λ x. t1) | = | {x}∪ BV(t1) |
| BV( t [ x/t' ] ) | = | {x}∪ BV(t)∪ BV(t') |
Comme dans le cas du λ-calcul, nous travaillerons modulo
α-conversion.
Définition 59 (Règles de réduction du λx-calcul)
Les règles de réductions du λx-calcul sont:
| (λ x. t) t' | → | t [ x/t' ] |
| x [ x/t ] | → | t |
| y [ x/t ] | → | y | si y≠ x |
| ( t1 t2) [ x/t' ] | → | t1 [ x/t' ] t2 [ x/t' ] |
| (λ y. t) [ x/t' ] | → | λ y. ( t [ x/t' ] ) | si
y≠ x |
Nous noterons →λx la relation engendrée par les règles
ci-dessus.
Lemme 60 (Confluence du λx-calcul [BR95])
La relation →λx est confluente.
Théorème 61 (Simulation [BG99])
Si t et t' sont deux λ-termes tels que t→λ t' alors
t—→λx+ t'.
Une conséquence de ce
théorème est la
non terminaison des λx-termes. Il nous faut donc donner un système
de types pour le λx-calcul. Pour cela, nous gardons la grammaire
des types (Définition 50) et nous étendons la
notion de λ-termes annotés aux λx-termes.
Définition 62 (Système de types pour le λx-calcul)
Les règles de typage du λx-calcul sont:
|
(Var) | si (x,A)∈Γ |
| |
| x : A,Γ⊢ t : B |
|
| Γ⊢λ x :
A. t :
A→B |
(Abs) |
| |
| Γ⊢ t1 : A→B Γ⊢ t2 :
A |
|
| Γ⊢ ( t1 t2) : B |
(App) |
| |
| Γ⊢ t' : B x : B,Γ⊢ t :
A |
|
| Γ⊢ t [ x/t' ] : A |
(Sub) | |
Théorème 63 (Préservation de types par réduction)
Soient t et t' deux λx-termes, Γ un environnement de
types et A un type. Si Γ⊢ t : A et t→λx t'
alors Γ⊢ t' : A.
-
- Preuve.
Par induction sur la structure de t puis par cas sur la règle de
réduction utilisée [Blo97].
Théorème 64 (Normalisation forte du λx-calcul simplement typé [Blo97])
Soient t un λx-terme, Γ un environnement de types, A un
type. Si Γ⊢ t : A alors t est fortement normalisable
pour la réduction →λx .