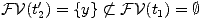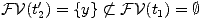Ce chapitre est consacré à la définition et à l'étude d'une extension
du λσ w-calcul aux motifs "à la ML" et au filtrage explicite. Le
système des filtres du λ Pw-calcul est inspiré des formalismes
précédents dans le domaine des filtres "à la
ML" [KPT96, CK99a, For02a, For02b]. Le λ Pw-calcul est, tout
comme le λσ w-calcul, un calcul dit "faible". Rappelons que les
calculs de substitution explicite faibles sont ceux pour lesquels il
n'existe pas de règle de réécriture de la forme
(λ x. M) [ s ] → λ x. ( M [ s ] ). Dans le
cas du λ Pw-calcul, il ne comportera pas de règle de la forme
(λ P. M) [ s ] → λ P. ( M [ s ] ) où P sera
un motif "à la ML". Cette particularité nous permettra de dénoter les
variables par des noms tout en n'utilisant pas l'α-conversion
dans le système de réduction. Un second avantage important de cette
absence sera de nous permettre de démontrer la terminaison de ce
calcul.
Le but principal de l'étude explicite de la substitution est de
permettre de rapprocher les calculs théoriques des implantations
pratiques. Le but poursuivi par l'étude explicite du filtrage
est le même. En effet, la plupart des langages de programmation
[LM92, Obj, HPJP92, Har02] et
des assistants de
preuve [Coq00, , Hal, ELA, Isa]
modernes utilisent cette fonctionnalité non primitive dans leur base
théorique actuelle.
Les principaux prédécesseurs du calcul λ Pw en matière de filtrage
"à la ML" dérivent du Calculus of Pattern
Matching [KPT96]. Ce calcul possédait des mécanismes de
filtrage et de substitution implicites. Serenella Cerrito et
Delia Kesner ont raffiné ce formalisme en proposant deux nouveaux
calculs [CK99a]. Le calcul TPC possède un
mécanisme de filtrage explicite et un mécanisme de substitution
implicite. Le calcul TPCES est une
extension de TPC à un système de substitution partiellement
explicite. Le système de substitution de
TPCES est fondé sur le système, très simple, de
substitutions du λx-calcul.
L'avancée majeur du λ Pw-calcul est d'être le premier formalisme à
proposer des systèmes de substitution et de filtrage
complètement explicite. A l'inverse de
TPCES, le λ Pw-calcul fonde son système de
substitutions sur le λσ w-calcul. L'inconvénient d'une telle
extension est la complexité très fortement accrue des concepts et des
preuves de propriétés par rapport au calcul
TPCES.
Le mécanisme de filtrage explicite du λ Pw-calcul sera obtenu par
l'ajout, en plus de la β-règle classique, d'un certain nombre de
règles de réécriture permettant de déconstruire les motifs jusqu'à
l'obtention d'une abstraction de la forme λ x. M. Ainsi, le
λ Pw-calcul comprendra une règle de réécriture de la forme:
| λ ⟨ P1, P2 ⟩. M ⟨ N1, N2 ⟩→
( λ P1. λ P2. M N1) N2
|
La suite de ce chapitre sera organisée de la manière suivante. La
section 4.1 sera consacrée à la définition des notions de
bases du λ Pw-calcul. Nous proposerons dans cette section une
grammaire pour les expressions ainsi que la démonstration de certaines
propriétés de base telles que la préservation de l'ensemble des
variables libres par réduction. La
section 4.2 sera alors consacrée à la
démonstration de la confluence du λ Pw-calcul sur l'ensemble de ses
expressions en utilisant une technique due à Tait et
Martin-Löf [Bar84] sur laquelle nous reviendrons dans la
présentation de cette section. Nous proposerons ensuite, dans la
section 4.3, un système de types avant de démontrer
la préservation de types par réduction. Enfin
la
section 4.4 sera consacrée à la preuve de normalisation
forte des expressions bien typées du λ Pw-calcul. Nous utiliserons au
cours de cette démonstration une extension de la méthode de preuve
dite "par réductibilité" dont nous présenterons les détails dans
l'introduction de cette section.
4.1 Définition du calcul
Cette section est consacrée à la définition du calcul λ Pw. Nous
présenterons tout d'abord sa grammaire dans la
sous-section 4.1.1, puis, dans la
sous-section 4.1.2, nous définirons
formellement les notions classiques de variables libres et liées dans
un terme. Nous proposerons alors des règles de réduction pour λ Pw.
Nous constaterons que la notion de variables libres n'est pas assez
fine car elle n'est pas préservée par réduction. La
sous-section 4.1.4 sera alors consacrée à la définition
de deux nouvelles notions: les variables libres localisées d'un
terme et les termes acceptables. Les termes acceptables
forment un sous-ensemble des termes qui préservent les variables
libres d'un terme par réduction. Enfin dans la sous
section 4.1.5 nous démontrerons les propriétés
de préservation de l'ensemble des variables libres et de la notion de
terme acceptable par réduction.
Le calcul λ Pw est une extension du λ-calcul classique. A ce
titre, la nécessité d'un système de types ayant de bonnes propriétés
est bien connue [Bar84]. Nous allons utiliser pour
définir λ Pw un système de types simples (c.f.
section 4.3).
Définition 1
Les types du λ Pw-calcul sont
donnés par la grammaire suivante:
| (Types) A | ::= | ι | Type de base |
| | ∣ | A× A | Type produit |
| | ∣ | A+A | Type somme |
| | ∣ | A→A | Type fonctionnel |
| |
Nous utiliserons, dans la suite de ce chapitre, les notations A,
B, C,…pour dénoter des types.
Contrairement à la famille des λ-calculs classiques qui ne
fournissent qu'un mécanisme d'abstraction sur les variables, λ Pw
fournit un mécanisme d'abstraction sur des motifs complexes.
Contrairement à la notion de motif du
ρ-calcul [CK98], ces motifs sont définis par
une grammaire indépendante de la grammaire des termes bien que
partageant avec celle-ci l'ensemble des variables.
Définition 2
Dans la grammaire des motifs qui suit, la variable
ξ
présente dans le constructeur de choix appartient à un nouvel
ensemble infini de variables disjoint de l'ensemble des variables
usuelles, l'ensemble des variable de choix. Cette variable
nous permettra de propager le résultat du choix fait sur un tel
motif tout au long de la réduction du terme auquel celui-ci
appartient.Les motifs du λ Pw-calcul sont donnés par la grammaire suivante:
| (Motif) P:= | | _ | Wildcard |
| | ∣ | x | Variable (usuelle) |
| | ∣ | ⟨ P, P ⟩ | Paire |
| | ∣ | @(P,P) | Contraction |
| | ∣ | | Choix |
| |
Les notations _ , x et ⟨ P, Q ⟩ sont des notations
classiques. La notation @(P,Q) est une généralisation du
constructeur as de OCAML. Le constructeur [ξ ∣ P,Q ] est le
constructeur de motif de choix tels que ceux présents dans la
construction function | P -> ... |Q -> ... de OCAML.
Les motifs seront, dans la suite de ce chapitre, dénotés par P, Q,
R,…
Définition 3
Un motif P est dit linéaire si et
seulement si chaque variable (usuelle ou de choix) apparaît au plus
une fois dans P.
Notation 4
Tout au long de ce chapitre nous utiliserons la notation P∈ Q
pour dénoter le fait que P est un sous motif de Q.
Nous sommes maintenant en mesure de définir la grammaire des
termes du calcul. Ces termes vont utiliser les motifs définis
précédemment dans leur mécanisme d'abstraction. Le calcul λ Pw
possédant un mécanisme explicite de substitution, nous aurons de plus
besoin de définir une grammaire pour les substitutions
explicites. Nous allons pour cela étendre la grammaire des
substitutions de λσ (c.f. chapitre 3). Enfin,
nous aurons besoin d'un troisième ensemble: l'ensemble de termes
de choix. Ce troisième ensemble nous permettra d'évaluer de
manière explicite les choix faits dans les motifs de choix.
Afin de préserver les "bonnes" propriétés de réduction pour λ Pw, nous
serons, dans la sous-section 4.1.4, conduits à
restreindre ces grammaires.
Définition 5 Les expressions du
λ Pw-calcul sont données par les grammaires suivantes:
| (Pré-substitution) s | ::= | id | Identité |
| | ∣ | ( x/M ).s | Constructeur usuel |
| | ∣ | ( ξP : A/K ).s | Constructeur de choix |
| | ∣ | s ∘ s | Concaténation |
| |
| (Pré-termes de choix) Ξ | ::= | ξ | Variable
de choix |
| | ∣ | L | Constante Gauche |
| | ∣ | R | Constante Droite |
| | ∣ | ξ [ s ] | Substitution de choix |
| |
| |
| (Pré-termes) M | ::= | x | Variable (usuelle) |
| | ∣ | M N | Application |
| | ∣ | ⟨ M, M ⟩ | Paire |
| | ∣ | inlB(M) | Injection gauche |
| | ∣ | inrA(M) | Injection droite |
| | ∣ | | Choix |
| | ∣ | | Choix suspendu |
| | ∣ | λ P : A. M | Abstraction |
| | ∣ | M [ s ] | Clôture |
| |
| |
Dans les définitions précédentes, L et R sont deux
constantes fixes du calcul. Nous utiliserons dans la suite la
notation K pour dénoter indifféremment l'une de ces deux
constantes. Nous utiliserons de même la notation T pour dénoter
indifféremment une constante de choix ou une variable de choix. De
même id est la substitution vide qui ne lie aucune variable.
La plupart des constructions présentes dans la définition des
pré-substitutions ou des pré-termes sont des constructions
classiques des λ-calculs avec substitutions explicites. La
construction Choix des termes est le pendant du constructeur
Choix des motifs. Plus intuitivement, un programme OCAML
ayant le squelette suivant:
function
| P1 -> M1
| P2 -> M2
pourra se "traduire" dans la présente grammaire par un pré-terme
de la forme λ [ξ ∣ P1,P2 ] :
A+B. [ξ ∣ M1,M2 ] où P1, P2, M1 et M2 sont les
traductions respectives de P1, P2, M1 et
M2. Les raisons de cette "séparation" entre les motifs et
leurs termes associés sont multiples. L'une d'entre elles est la
possibilité de lier de manière unique des variables dans les deux
termes d'une alternative. En effet, un pré-terme de la forme
λ [ξ ∣ P1,P2 ] : A+B. λ P3 :
C. [ξ ∣ M1,M2 ] est un pré-terme appartenant à notre
grammaire qui lie le motif P3 à la fois dans le pré-terme M1
et dans le pré-terme M2. Nous voyons ici la nécessité des
variables de choix qui vont nous permettre dans ce cas de déterminer
quel motif de choix lie le pré-terme de choix [ξ ∣ M1,M2 ].
En effet le motif P3 peut lui aussi contenir un motif de choix.
Notation 6
Tout au long de cette section nous utiliserons la notation
( ξQ : A/K )∈ s pour dénoter le fait que
( ξQ : A/K ) est une sous pré-substitution de
s.De plus, nous utiliserons dans la suite de ce chapitre les notations
suivantes:
-
s, t, u, …désignerons des pré-substitutions.
- M, N, …désignerons des pré-termes.
- Ξ, Ψ,…désignerons des pré-termes de choix.
Dans un souci de simplification des notations nous omettrons les types
présents dans ces grammaires quand leur présence ne sera pas
nécessaire à la compréhension.
Notation 7
Dans la suite de cette étude nous appellerons indifféremment
pré-expression un pré-terme, une pré-substitution ou un
pré-terme de choix.
Nous allons maintenant définir les notions de variables libres
et liées d'une pré-expression.
4.1.2 Variables libres et liées
Comme toujours dans les λ-calculs utilisant des variables nommées,
nous travaillerons modulo α-conversion. Nous donnons maintenant
la définition formelle des variables liantes d'un motif et
d'une pré-substitution par induction sur la structure de ces derniers.
Définition 8 (Variables liées par une substitution ou un motif)
L'ensemble des variables liées par une substitution ou
par un motif
est défini comme suit:
| Var( _ ) | = | ∅ |
| Var(x) | = | { x } |
| Var(⟨ P, Q ⟩) | = | Var(P) ∪ Var(Q) |
| Var([ξ ∣ P,Q ]) | = | Var(P) ∪ Var(Q) ∪ { ξ } |
| Var(@(P, Q)) | = | Var(P)∪ Var(Q) |
| Var(id) | = | ∅ |
| Var(( x/M ).s) | = | Var(s)∪ {x} |
| Var(( ξP/K ).s) | = | Var(s)∪ Var(P)∪ { ξ} |
| Var(s ∘ t) | = | Var(s)∪ Var(t) |
A titre d'exemple, la définition précédente nous permet d'obtenir:
| = | {ξ,x,y} |
| et |
| Var(( x/M ).( ξy/L ).id) | = | {x,y,ξ} |
|
Nous sommes maintenant en mesure de définir les variables
libres d'une pré-expression. Informellement ce sont les variables
présentes dans cette expression qui ne sont pas liées dans
celle-ci.
Définition 9 (Variables libres)
Nous définissons les variables libres d'une pré-expression par induction
sur la structure des expressions comme suit:
| FV(x) | | = | { x } |
| FV(inl(M))= FV(inr(M)) | | = | FV(M) |
| FV( M N) = FV(⟨ M, N ⟩) | | = | FV(M) ∪ FV(N) |
| FV(λ P. M) | | = | FV(M) ∖ Var(P) |
| FV( M [ s ] ) | | = | ( FV(M)∖
Var(s))∪ FV(s) |
| FV([ξ ∣ M,N ]) | | = | FV(M) ∪ FV(N) ∪ {ξ} |
| FV([Ξ ∣ s M,N ]) | | = | FV( M [ s ] )∪ FV( N [ s ] )∪ FV(Ξ) |
| FV(id)= FV(K) | | = | ∅ |
| FV(( x/M ).s) | | = | FV(M)∪ FV(s) |
| FV(( ξP/K ).s) | | = | FV(s) |
| FV(s ∘ t) | | = | ( FV(s)∖ Var(t))∪ FV(t) |
| FV(ξ) | | = | {ξ} |
|
FV( ξ [ s ] ) | | = | ({ξ}∖ Var(s))∪
FV(s) |
Nous noterons dans la suite FCV(e) le sous ensemble des variables
libres de e ne contenant que des variables de choix.
Définition 10 (Variables liées d'une expression)
L'ensemble des variables
liées d'une pré-expression e est l'ensemble des variables
apparaissant dans e qui ne sont pas libres dans e.
Ainsi nous avons par exemple:
| FV(λ [ξ ∣ x,y ]. [ψ ∣ x,t ]) | = | {ψ,t} |
| FV(λ [ξ ∣ x,y ]. [ξ ∣ y,x ]) | = | ∅ |
4.1.3 Règles de réduction
Nous somme maintenant en mesure de définir les règles de réduction de
λ Pw. Afin de faciliter la lecture de ces règles nous les avons
regroupées en différents ensembles. Le premier ensemble Départ
nous permet de ne pas dédoubler les règles du second, l'ensemble Filtrage, qui est l'ensemble des règles qui effectuent le filtrage
d'un terme par un motif. L'ensemble Choix est l'ensemble des
règles permettant d'évaluer un choix dans un terme. Les autres
ensembles sont des extensions naturelles des règles du calcul λσ w
(c.f. chapitre 3). Nous avons omis les types de
cette présentation.
| Départ |
| (λ P. M) N | → | (λ P. M) [ id ] N | (Abs_id) |
| Filtrage |
|
(λ ⟨ P1, P2 ⟩. M) [ s ] ⟨ N1, N2 ⟩ | → | ( (λ P1. λ P2. M) [ s ] N1) N2 | (Abs_pair) |
|
(λ @(P1,P2). M) [ s ]
N | → | ( (λ P1. λ P2. M) [ s ] N)
N | (Abs_contr) |
|
(λ [ξ ∣ P1,P2 ]. M) [ s ]
inl(N) | → | (λ P1. M) [ ( ξP2/L ).s ]
N | (Abs_left) |
|
(λ [ξ ∣ P1,P2 ]. M) [ s ]
inr(N) | → | (λ P2. M) [ ( ξP1/R ).s ]
N | (Abs_right) |
|
(λ x. M) [ s ] N | → | M [ ( x/N ).s ] | (Abs_var) |
|
(λ _ . M) [ s ] N | → | M [ s ] | (Abs_wild) |
| Choix |
| [ξ ∣ M,N ] [ s ] | → | [ ξ [ s ] ∣ s M,N ] | (Freeze) |
| [L ∣ s M,N ] | → | M [ s ] | (Left) |
| [R ∣ s M,N ] | → | N [ s ] | (Right) |
| [ξ ∣ s M,N ] | → | [ξ ∣ M [ s ] , N [ s ] ] | (Xi) |
| Propagation des substitutions |
| ( M N) [ s ] | → | M [ s ] N [ s ] | (app) |
| inl(M) [ s ] | → | inl( M [ s ] ) | (left) |
| inr(M) [ s ] | → | inr( M [ s ] ) | (right) |
| ⟨ M1, M2 ⟩ [ s ] | → | ⟨ M1 [ s ] , M2 [ s ] ⟩ | (pair) |
| Substitutions, Variables et Constantes |
| x [ id ] | → | x | (var1) |
| x [ ( x/N ).s ] | → | N | (var2) |
| y [ ( x/N ).s ] | → | y [ s ] si y≠
x | (var3) |
| x [ ( ξP/K ).s ] | → | x [ s ] | (var4) |
| ξ [ id ] | → | ξ | (sum_var1) |
| ξ [ ( ξP/K ).s ] | → | K | (sum_var2) |
| ξ [ ( ψP/K ).s ] | → | ξ [ s ]
si ξ≠ψ | (sum_var3) |
| ξ [ ( x/M ).s ] | → | ξ [ s ] | (sum_var4) |
| Substitutions et Composition |
| M [ s ] [ t ] | → | M [ s ∘ t ] | (clos) |
| (s ∘ t) ∘ u | → | s ∘ (t ∘ u) | (ass_env) |
| (( x/M ).s) ∘ t | → | ( x/ M [ t ] ).(s ∘ t) | (concat1) |
| (( ξP/K ).s) ∘ t | → | ( ξP/K ).(s ∘ t) | (concat2) |
| id ∘ s | → | s | (id) |
Les règles (Abs_left) et (Abs_right) justifient la présence d'un
motif dans la construction de choix des substitutions. En effet, si
cette construction était simplement de la forme
( ξ/K ).s, ces deux règles libéreraient les variables
liées par le motif non choisi.
Considérons en effet les termes:
| t1 =def λ [ξ ∣ x,y ]. [ξ ∣ x,y ] inl (M) |
| et |
| t2 =def λ x. [ξ ∣ x,y ] [ ( ξy/L ).id ] M |
Nous remarquons tout d'abord que t1—→* t2 et que nous avons
bien FV(t2)⊂ FV(t1). En revanche, si nous "oublions" le
motif y dans le terme t2 et si nous considérons donc le terme
t2'=def
λ x. [ξ ∣ x,y ] [ ( ξ/L ).id ] M,
nous avons alors
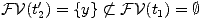
Notation 11
Le système de réduction engendré par les règles des groupes (Départ) et (Filtrage) qui sont utilisées pour implanter le
filtrage sera par la suite noté →P . Les autres règles, qui
implantent la gestion de la substitution, génèrent un système de
réduction noté dans la suite →es . Quand la distinction sera
nécessaire nous utiliserons la notation →λ Pw pour le système de
réduction engendré par l'ensemble de toutes les règles. Le reste du
temps nous utiliserons simplement la notation → pour ce système
de réduction.
Nous remarquons alors que suivant ces règles, la réduction suivante
est possible:
| t1 | = | (λ [ξ ∣ x,y ]. [ξ ∣ y,x ]) [ id ] inl (M) |
| | → | (λ x. [ξ ∣ y,x ]) [ ( ξy/L ).id ] M |
| | → | [ξ ∣ y,x ] [ ( x/M ).( ξy/L ).id ] |
| | → | [ ξ [ ( x/M ).( ξy/L ).id ] ∣ ( x/M ).( ξy/L ).id y,x ] |
| | —→* | [L ∣ ( x/M ).( ξy/L ).id y,x ] |
| | → | y [ ( x/M ).( ξy/L ).id ] |
| | —→* | y |
Cet exemple nous montre un premier problème: la notion de variables
libres n'est dans notre cadre pas assez restrictive pour pouvoir être
préservée par réduction. En effet si dans le terme
λ [ξ ∣ x,y ]. [ξ ∣ y,x ] qui ne contient pas de
variables libres, nous effectuons le choix L nous obtiendrons un
terme de la forme λ x. y dans lequel la variable y est
libre.
Afin de résoudre ce problème nous allons proposer une nouvelle notion
de variable libre: les variables libres localisées.
4.1.4 Variables libres localisées et termes acceptables
L'ensemble des variables libres localisées d'une pré-expression
e par rapport à une variable de choix ξ et à un choix K
peut être compris informellement comme l'ensemble des variables qui
resteraient libres dans e après tout remplacement de ξ par
la valeur K:
FVξK(e)≡ FV(e{ ξ ← K } ).
Définition 12 (Variables libres localisées)
Étant donné une variable de choix ξ et une constante de
choix K, nous définissons l'ensemble des variables libres localisées de e par
rapport à ξ et au choix K par induction sur e comme
suit:
| FVξK(x) | = | { x } |
| FVξK(inl(M)) | = | FVξK(M) |
| FVξK(inr(M)) | = | FVξK(M) |
| FVξK( M N) | = | FVξK(M) ∪ FVξK(N) |
| FVξK(⟨ M, N ⟩) | = | FVξK(M) ∪ FVξK(N) |
| FVξK(λ P. M) | = | FVξK(M) ∖ Var(P) |
| FVξK( M [ s ] ) | = | ( FVξK(M)∖ Var(s))∪ FVξK(s) |
| FVξL([ξ ∣ M,N ]) | = | FVξL(M) |
| FVξR([ξ ∣ M,N ]) | = | FVξR(N) |
| FVξK([ψ ∣ M,N ]) | = | FVξK(M) ∪ FVξK(N) ∪ {ψ} |
| FVξL([ξ ∣ s M,N ]) | = | ( FVξL(M)∖ Var(s))∪ FVξL(s) |
| FVξR([ξ ∣ s M,N ]) | = | ( FVξR(N)∖ Var(s))∪ FVξR(s) |
| FVξK([ψ ∣ s M,N ]) | = | ( FVξK(M)∪ FVξK(N))∖Var(s) |
| | | ∪ FVξK(s) ∪{ψ} |
| FVξK([K' ∣ s M,N ]) | = | ( FVξK(M)∪ FVξK(N))∖ Var(s) |
| | | ∪ FVξK(s) |
| FVξK([ ψ [ s' ] ∣ s M,N ]) | = | ( FVξK(M)∪ FVξK(N))∖ Var(s) |
| | | ∪ FVξK(s) ∪ FVξK( ψ [ s' ] ) |
| FVξK([ ξ [ s' ] ∣ s M,N ]) | = | (( FVξK(M)∪ FVξK(N))∖ Var(s)) |
| | | ∪ FVξK(s)∪
FVξK( ξ [ s' ] )
si ξ∈Var(s') |
| FVξL([ ξ [ s' ] ∣ s M,N ]) | = | ( FVξL(M)∖ Var(s)) |
| | | ∪ FVξR(s)∪
FVξR( ξ [ s' ] )
si ξ∉Var(s') |
| FVξR([ ξ [ s' ] ∣ s M,N ]) | = | ( FVξR(M)∖ Var(s)) |
| | | ∪ FVξR(s)∪
FVξR( ξ [ s' ] )
si ξ∉Var(s') |
| FVξK(id)= FVξK(K) | = | ∅ |
| FVξK(( x/M ).s) | = | FVξK(M)∪ FVξK(s) |
| FVξK(( ξP/K ).s) | = | FVξK(s) |
| FVξK(s ∘ t) | = | ( FVξK(s)∖ Var(t))∪ FVξK(t) |
| FVξK(ξ) | = | {ξ} |
|
FVξK( ξ [ s ] ) | = | ({ξ}∖ Var(s))∪ FVξK(s) |
Dans la précédente définition nous supposons que
ψ≠ξ.
Ainsi nous avons:
| FVξL(λ [ξ ∣ x,y ]. [ξ ∣ x,t ]) | = | ∅ |
| FVξL(λ y. [ξ ∣ x,t ]) | = | {x} |
| FVξK( x [ ( ξx/L ).id ] ) | = | ∅ |
| FVξL([ξ ∣ y,x ]) | = | {y} |
Remarque 13
Étant donné une pré-expression e, une variable de choix ξ
et une constante de choix K, les deux résultats suivants sont
vrais:
-
FVξL(e) ⊂ FV(e) .
- Si de plus ξ n'est pas une variable libre de e alors
l'inclusion précédente devient une égalité.
-
- Preuve.
La preuve est immédiate par induction sur l'expression e.
Définissons maintenant formellement la notion de pré-expression
acceptable. Le rôle de la notion de pré-expression acceptable est
de capturer les pré-expressions pouvant libérer des variables lors
de leur réduction. Intuitivement, le pré-terme
λ [ξ ∣ x,y ]. [ξ ∣ y,x ] n'est pas acceptable.
Définition 14 (pré-expressions acceptables)
Nous définissons l'ensemble des pré-expressions acceptables comme étant le plus
petit ensemble de pré-expressions contenant les variables usuelles,
les constantes de choix, la constante id et clos par sous
expression tel que:
| Acc( ψ [ s ] ) | si | ∀ ( ξQ/K )∈ s, ψ ∉Var(Q) | |
| Acc( M [ s ] ) | si | ∀ ( ξQ/K )∈ s, FVξK(M)∩ Var(Q)=∅ | |
| Acc(s ∘ t) | si | ∀ ( ξQ/K )∈ t, FVξK(s)∩ Var(Q)=∅ | |
| Acc(λ P. M) | si | ∀[ξ ∣ Q1,Q2 ]∈ P,{ | FVξR(M)⋂ Var(Q1) | = | ∅ |
| FVξL(M)⋂ Var(Q2) | = | ∅ |
| |
| Acc([ξ ∣ s M,N ]) | si | Acc( M [ s ] ) et Acc( N [ s ] ) | |
| Acc([ ξ [ t ] ∣ s M,N ]) | si | ( ξQ/K )∉t, Acc( M [ s ] ) et
Acc( N [ s ] ) et Acc( ξ [ t ] ) | |
| Acc([ ξ [ t ] ∣ s M,N ]) | si | ( ξQ/L )∈ t, Acc( M [ s ] )
et Acc( ξ [ t ] ) | |
| Acc([ ξ [ t ] ∣ s M,N ]) | si | ( ξQ/R )∈ t, Acc( N [ s ] )
et Acc( ξ [ t ] ) | |
| Acc([L ∣ s M,N ]) | si | Acc( M [ s ] ) | |
| Acc([R ∣ s M,N ]) | si | Acc( N [ s ] ) | |
Ainsi le pré-terme λ [ξ ∣ x,y ]. [ψ ∣ x,t ]
n'est pas acceptable par définition de Acc( ) pour les abstractions
. En effet,
FVξR([ψ ∣ x,t ])={x,t,ψ}
et Var(x)={x}.
Définition 15
Nous utiliserons appellerons désormais termes (resp.
substitution, terme de choix et expression) un
pré-terme (resp. une pré-substitution, un pré-terme de
choix ou une pré-expression) acceptable.
Remarque 16
Les pré-termes [ξ ∣ M1,M2 ] [ s ] et
[ ξ [ t1 ] ∣ t2 M1,M2 ] [ s ] ne
sont des termes que si et seulement si ∀
( ψP/K )∈ s, ξ∉Var(P) (ou si
ξ∈Var(t1) dans le second cas).
Nous allons maintenant démontrer que les variables libres (localisées)
et les termes acceptables sont préservés par réduction.
4.1.5 Correction de λ Pw
Nous allons tout d'abord démontrer que les variables libres localisées
sont préservées par réduction mais avant toute chose nous remarquons
que:
Remarque 17
Si s et t sont deux pré-substitutions telles que s→ t alors
Var(s)=Var(t).
Lemme 18 (Préservation des variables libres
localisées) Soient e et e' deux
pré-expressions telles que e→ e'. Si e est une expression,
ξ est une variable de choix et K une constante de choix
alors:
-
- Preuve.
Tout d'abord nous remarquons que, par α-conversion, nous
pouvons supposer que ξ n'apparaît pas liée dans e. La
preuve est alors faite par induction sur la structure des
expressions et par cas sur la règle de réduction utilisée.
-
Si e=x, e=id, e=L, e=R ou e=ξ, le
résultat est immédiat puisque e ne possède pas de réduit.
- Si e=( x/M ).s ou e=( ξP/K' ).s,
e n'étant pas réductible en tête, le résultat est immédiat par
hypothèse d'induction.
- Si e=s ∘ t,
5 possibilités
s'offrent à nous.
-
Si la réduction n'a pas lieu en tête, le résultat est
immédiat par la remarque 17 et par
hypothèse d'induction.
- Si s=id et e' =t, le résultat est immédiat.
- Si s=( ψQ/K' ).u et
e'=( ψQ/K' ).(u ∘ t), nous avons
alors:
| FVξK(e) | = | ( FVξK(( ψQ/K' ).u)∖
Var(t)) ⋃ FVξK(t) |
| | = | ( FVξK(u)∖ Var(t)) ⋃ FVξK(t) |
| | = | FVξK(u ∘ t) |
| | = | FVξK(( ψQ/K' ).(u ∘ t)) |
| | = | FVξK(e') |
| |
|
- Si s=( x/M ).u et
e'=( x/ M [ t ] ).(u ∘ t), nous avons alors:
| FVξK(e) | = | ( FVξK(( x/M ).u)
∖ Var(t)) ⋃
FVξK(t) |
| | = | (( FVξK(M) ⋃ FVξK(u))∖ Var(t)) ⋃ FVξK(t) |
| | = | ( FVξK(M)∖ Var(t)) ⋃
(( FVξK(u)∖ Var(t)) |
| | | ⋃ FVξK(t)) |
| | = | ( FVξK(M)∖ Var(t)) ⋃
FVξK(u ∘ t) |
| | = | FVξK(( x/ M [ t ] ).(u ∘ t)) |
| | = | FVξK(e') |
| |
|
- Si
s=s1 ∘ s2 et e'=s1 ∘ (s2 ∘ t),
nous avons alors:
| FVξK(e) | = | ( FVξK(s1 ∘ s2)
∖ Var(t))
⋃ FVξK(t) |
| | = | ⎛
⎝ | (( FVξK(s1)∖ Var(s2))⋃ FVξK(s2) ) ∖ Var(t) | ⎞
⎠ |
|
| | | ⋃ FVξK(t) |
| | = | ⎛
⎝ | FVξK(s1)∖ (Var(s2)⋃
Var(t)) | ⎞
⎠ | ⋃ |
|
| | | ⎛
⎝ | ( FVξK(s2) ∖ Var(t)) ⋃ FVξK(t) | ⎞
⎠ |
|
| | = | ( FVξK(s1)∖ Var(s2 ∘ t))
⋃
FVξK(s2 ∘ t) |
| | = | FVξK(e') |
| |
|
- Si e= ξ' [ s ] ,
4 possibilités
s'offrent alors à nous:
-
Si e'= ξ' [ s' ] avec s→ s', le résultat
est alors immédiat par la remarque 17
et par hypothèse d'induction.
- Si s=id et e'=ξ' ou si
s=( ξ'Q/K' ).t et e'=K' le résultat est
immédiat.
- Si s=( ψQ/K' ).t avec
ψ≠ξ' et e'= ξ' [ t ] nous
remarquons tout d'abord que, puisque e est acceptable nous
avons:
| ∀ (ψ'Q'/K)∈
( ψQ/K' ).t, ξ' ∉Var(Q')
|
Nous en déduisons en particulier que ξ'∉Var(Q)
et donc que:
| FVξK(e) | = | ({ξ'}∖
({ψ}⋃ Var(Q)⋃ Var(t))) ⋃
FVξK(t) |
| | = | ({ξ'}∖ Var(t)) ⋃
FVξK(t) puisque
ξ'∉{ψ}⋃Var(Q) |
| | = | FVξK(e') |
| |
|
- Si
s=( x/M ).t et e'= ξ' [ t ] nous avons:
| FVξK(e) | = | (ξ'∖ (Var(t)⋃
{x})) ⋃
FVξK(( x/M ).t) |
| | = | (ξ'∖ Var(t)) ⋃ ( FVξK(M)
⋃
FVξK(t)) |
| | ⊇ | (ξ'∖ Var(t)) ⋃
FVξK(t) |
| | = | FVξK(e') |
| |
|
- Si e=( M N),
8 possibilités
s'offrent alors à nous:
-
Si la réduction n'a pas lieu en tête, le résultat est
immédiat par hypothèse d'induction.
- Si e=λ P. M1 et e'= (λ P. M1) [ id ]
N, le résultat est immédiat.
- Si e= (λ ⟨ P1, P2 ⟩. M1) [ s ] , N=⟨ N1, N2 ⟩ et
e'=( (λ P1. λ P2. M1) [ s ] N1) N2
nous remarquons que par α-conversion nous pouvons
supposer que Var(s)∩ (Var(P1)∪ Var(P2)) =
∅ et que nous avons donc:
| FVξK(e) | = | FVξK( (λ ⟨ P1, P2 ⟩. M1) [ s ] )⋃ FVξK(⟨ N1, N2 ⟩) |
| | = | (
( FVξK(λ ⟨ P1, P2 ⟩. M1)∖
Var(s)) ⋃ FVξK(s)) ⋃ |
| | | ( FVξK(N1) ⋃
FVξK(N2)) |
| | = | (( FVξK(M1)∖ (Var(P1)⋃
Var(P2)))
∖ Var(s)) ⋃ |
| | | FVξK(s) ⋃ ( FVξK(N1) ⋃
FVξK(N2)) |
| | = | (( FVξK(M1)∖ Var(P2))∖
Var(P1))
∖ Var(s))⋃ |
| | | FVξK(s) ⋃ ( FVξK(N1) ⋃
FVξK(N2)) |
| | = | ((( FVξK(λ P2. M1))∖
Var(P1))
∖ Var(s)) ⋃ |
| | | FVξK(s) ⋃ ( FVξK(N1) ⋃
FVξK(N2)) |
| | = | ((( FVξK(λ P1. λ P2. M1))
∖ Var(s)) ⋃ FVξK(s)) ⋃ |
| | | ( FVξK(N1) ⋃
FVξK(N2)) |
| | = | (( FVξK( (λ P1. λ P2. M1) [ s ] ))
⋃ FVξK(N1)) ⋃
FVξK(N2) |
| | = | ( FVξK( (λ P1. λ P2. M1) [ s ]
N1))⋃ FVξK(N2) |
| | = | ( FVξK( (λ P1. λ P2. M1) [ s ]
N1) N2) |
| | = | FVξK(e') |
| |
|
- Si e= (λ @(P1,P2). M1) [ s ] et
e'=( (λ P1. λ P2. M1) [ s ] N) N nous
raisonnons comme dans le cas précédent.
- Si e= (λ [ψ ∣ P1,P2 ]. M1) [ s ] , N=inl (N1) et
e'= (λ P1. M1) [ ( ψP2/L ).s ]
N1 alors, une fois encore par α-conversion nous pouvons
supposer que Var(s)∩ (Var(P1)∪ Var(P2)∪
{ψ}) = ∅, et nous avons donc:
|
FVξK(e) | = | | FVξK( (λ | ⎡
⎣ | ψ ∣ P1,P2 | ⎤
⎦ | . M1) [ s ] )⋃
FVξK(N1) |
|
| | = | | (( FVξK(λ | ⎡
⎣ | ψ ∣ P1,P2 | ⎤
⎦ | . M1)∖
Var(s)) ⋃ FVξK(s)) |
|
| | | ⋃ FVξK(N1) |
| | = | ( FVξK(M1) ∖ ({ψ}⋃
Var(P1)
⋃ Var(P2))∖ Var(s)) |
| | | ⋃ FVξK(s) ⋃ FVξK(N1) |
| | = | ( FVξK(M1) ∖ Var(P1) ∖
({ψ}⋃ Var(P2) ⋃ Var(s))) |
| | | ⋃ FVξK(s) ⋃ FVξK(N1) |
| | = | (( FVξK(λ P1. M1)∖
({ψ}⋃
Var(P2) ⋃ Var(s))) ⋃ |
| | | FVξK(s)) ⋃ FVξK(N1) |
| | = | FVξK( (λ P1. M1) [ ( ψP2/L ).s ] )
⋃ FVξK(N1) |
| | = | FVξK( (λ P1. M1) [ ( ψP2/L ).s ] N1) |
| | = | FVξK(e') |
| |
|
- Si e= (λ [ψ ∣ P1,P2 ]. M1) [ s ] ,
N=inr (N1) et
e'= (λ P2. M1) [ ( ψP1/R ).s ]
N1 nous raisonnons comme dans le cas précédent.
- Si M= (λ x. M1) [ s ] et si de plus
e'= M1 [ ( x/N ).s ] , nous avons alors:
|
FVξK(e) | = | FVξK( (λ x. M1) [ s ] )
⋃
FVξK(N) |
| | = | (( FVξK(λ x. M1)∖
Var(s))⋃ FVξK(s) ) |
| | | ⋃
FVξK(N) |
| | = | ((( FVξK(M1)∖ {x})∖
Var(s))⋃ FVξK(s) ) |
| | | ⋃
FVξK(N) |
| | = | ( FVξK(M1)∖ (Var(s)⋃ {x}))⋃
FVξK(s) |
| | | ⋃
FVξK(N) |
| | = | FVξK( M1 [ ( x/N ).s ] ) |
| | = | FVξK(e') |
| |
|
- Si
e= (λ _ . M1) [ s ] et e'= M1 [ s ]
nous avons:
| FVξK(e) | = | FVξK( (λ _ . M1) [ s ] )
⋃
FVξK(N) |
| | = | (( FVξK(λ _ . M1)∖
Var(s))⋃ FVξK(s) ) ⋃
FVξK(N) |
| | = | ((( FVξK(M1)∖ ∅)∖
Var(s))⋃ FVξK(s) ) ⋃
FVξK(N) |
| | ⊇ | ( FVξK(M1)∖ Var(s))⋃ FVξK(s) |
| | = | FVξK( M1 [ s ] ) |
| | = | FVξK(e') |
| |
|
- Si e=⟨ M1, M2 ⟩, e=inl (M1), e=inr (M1),
e=[ψ ∣ M,N ] le résultat est immédiat par hypothèse d'induction
puisque e ne possède par de réduit en tête.
- Si e=[Ξ ∣ s M1,M2 ],
6 possibilités
s'offrent a nous:
-
Si la réduction n'a pas lieu en tête, le résultat est
immédiat par la remarque 17 et par
hypothèse d'induction.
- Si Ξ=L et e'= M1 [ s ] nous avons alors:
| FVξK(e) | = | (( FVξK(M1)⋃ FVξK(M2))∖ Var(s))⋃ FVξK(s) |
| | ⊇ | ( FVξK(M1)∖ Var(s))⋃ FVξK(s) |
| | = | FVξK(e') |
| |
|
- Si Ξ=R et e'= M2 [ s ] , nous raisonnons
comme dans le cas précédent.
- Si K=L, Ξ=ξ et
e'=[ξ ∣ M1 [ s ] , M2 [ s ] ] nous avons:
| FVξL(e) | = | ( FVξL(M1)∖Var(s))⋃ FVξL(s) |
| | = | FVξL( M1 [ s ] ) |
| | = | FVξL(e') |
| |
|
- Si K=R, Ξ=ξ et
e'=[ξ ∣ M1 [ s ] , M2 [ s ] ], nous raisonnons
comme dans le cas précédent.
- Si
Ξ=ψ, ψ≠ξ et
e'=[ψ ∣ M1 [ s ] , M2 [ s ] ] nous
avons:
| FVξK(e) | = | |
| | = | (( FVξK(M1)⋃ FVξK(M2))∖
Var(s))⋃ FVξK(s)
⋃ {ψ} |
| | = | (( FVξK(M1)∖ Var(s))⋃
FVξK(s))⋃ |
| | | (( FVξK(M2)∖Var(s))⋃ FVξK(s)) ⋃ {ψ} |
| | = | FVξK( M1 [ s ] )⋃ FVξK( M2 [ s ] )⋃{ψ} |
| | = | FVξL(e') |
| |
|
- Si e=λ P. M le résultat est immédiat par hypothèse d'induction puisque
e ne possède pas de réduit en tête.
- Si e= M [ s ] ,
4 possibilités
s'offrent alors à nous:
-
Si la réduction n'a pas lieu en tête, le résultat est
immédiat par la remarque 17 et par
hypothèse d'induction.
- Si M= M1 M2 et
e'= M1 [ s ] M2 [ s ] nous avons alors:
| FVξK(e) | = | ( FVξK((M1
M2))∖ Var(s)) ⋃
FVξK(s) |
| | = | (( FVξK(M1)⋃ FVξK(M2))∖
Var(s)) ⋃
FVξK(s) |
| | = | (( FVξK(M1))∖ Var(s)) ⋃
FVξK(s))
⋃ |
| | | (( FVξK(M2)∖ Var(s)) ⋃
FVξK(s)) |
| | = | FVξK( M1 [ s ] ) ⋃ FVξK( M1 [ s ] ) |
| | = | FVξK(e') |
| |
|
- Si M=⟨ M1, M2 ⟩ et
e'=⟨ M1 [ s ] , M2 [ s ] ⟩, M=inl (M1) et
e'=inl ( M1 [ s ] ) ou M=inr (M1) et
e'=inr ( M1 [ s ] ), nous raisonnons comme dans le cas
précédent.
- Si M=x,
s=id et e'=x, si M=x, s=( x/N ).t et e'=N, si
M=x, s=( y/N ).t, x≠ y et e'= x [ t ] , ou si
M=x, s=( ψQ/K' ).t et
e'= x [ t ] , le résultat est immédiat puisque e est
acceptable.
De ce lemme et de la remarque 13, nous
déduisons la propriété fondamentale:
Corollaire 19
Si e1 et e2 sont deux pré-expressions telles que e1 soit
acceptable et e1→ e2, alors FV(e2)⊂ FV(e1).
-
- Preuve.
Il suffit de prendre une variable de choix ξ n'appartenant
ni à e1 ni à e2.
Afin de pouvoir ne travailler que sur des pré-expressions acceptables,
il nous faut prouver la stabilité de cet ensemble par réduction.
Lemme 20 (Correction de la notion d'acceptabilité)
Si e est une expression telle que e→ e ', alors e ' est
elle-même une expression.
-
- Preuve.
Nous allons démontrer ce lemme en raisonnant par induction sur la
structure de e et par cas sur la règle utilisée pour atteindre e
'. Nous ne traiterons dans cette preuve ni les cas où e ne
possède pas de réduit, ni les cas où la réduction ne s'effectue pas
en tête d'expression. Dans ce dernier cas, nous obtenons le résultat
par hypothèse d'induction et par le lemme 18.
-
Si la règle utilisée est la règle (Abs_id), alors nous
devons avoir e= λ P. M N donc nous savons que
λ P. M et N sont acceptables. Nous en déduisons
aisément que (λ P. M) [ id ] l'est aussi d'où le
résultat.
- Si la règle utilisée est la règle (Abs_pair), alors e= (λ ⟨ P1, P2 ⟩. M) [ s ]
⟨ N1, N2 ⟩. Par α-conversion nous pouvons supposer
que Var(s)∩ (Var(P1)∪ Var(P2))=∅ et nous
en déduisons que :
- [(R1)]
M, s, N1 et N2 sont acceptables.
- (λ ⟨ P1, P2 ⟩. M) [ s ] est acceptable
d'où
| ∀ ( ξQ/K )∈ s,
FVξK(λ ⟨ P1, P2 ⟩. M) ⋂
Var(Q)=∅ |
ou de manière équivalente
| ∀ ( ξQ/K )∈ s,
( FVξK(M) ∖ (Var(P1)⋃ Var(P2)))
⋂ Var(Q)=∅ (*)
|
- λ ⟨ P1, P2 ⟩. M est acceptable d'où
| ∀ | ⎡
⎣ | ξ ∣ Q1,Q2 | ⎤
⎦ | ∈ ⟨ P1, P2 ⟩, | ⎧
⎪
⎨
⎪
⎩ | | ( FVξR(M) ⋂ Var(Q1))=∅ |
| et |
| ( FVξL(M)⋂ Var(Q2)) = ∅ |
|
|
Puisque N2 est acceptable, il nous suffit de montrer que
(λ P1. λ P2. M) [ s ] N1 est
acceptable. Puisque N1 est acceptable, il nous suffit de
montrer que (λ P1. λ P2. M) [ s ] est
acceptable. Pour montrer ce dernier point, nous devons:
-
Montrer que ∀ ( ξQ/K )∈
s, FVξK(λ P1. λ P2. M) ∩
Var(Q)=∅. Or nous savons que
FVξK(λ P1. λ P2. M)= FVξK(M)
∖ (Var(P1) ∪ Var(P2)) et nous obtenons le
résultat par (*).
- Monter que λ P1. λ P2. M est acceptable,
i.e. montrer que λ P2. M est acceptable et que
∀ [ξ ∣ Q1,Q2 ]∈ P1,
FVξR(λ P2. M) ∩
Var(Q1)=∅ et
FVξL(λ P2. M)∩ Var(Q2) =
∅. Nous ne donnons ici que la preuve de ces deux
dernières égalités, la preuve d'acceptabilité de
λ P2. M étant du même type. Nous remarquons que si
[ξ ∣ Q1,Q2 ]∈ P1 alors [ξ ∣ Q1,Q2 ]∈⟨ P1, P2 ⟩.
Nous obtenons alors le résultat recherché par R3 en remarquant
de plus que
FVξK(λ P2. M)⊂ FVξK(M).
- Si la règle utilisée est la règle (Abs_contr), nous
raisonnons comme dans le cas précédent.
- Si la règle utilisée est la règle (Abs_left),
alors e= (λ [ψ ∣ P1,P2 ]. M) [ s ]
inl(N) d'où nous déduisons que:
- [(R1)]
Par α-conversion, nous pouvons supposer que (Var(P1)
∪ Var(P2) ∪ {ψ}))∩ Var(s)=∅.
-
M, N et s sont acceptables.
- (λ [ψ ∣ P1,P2 ]. M) [ s ] est
acceptable, c'est à dire:
| ∀ ( ξQ/K )∈ s,
FVξK(λ | ⎡
⎣ | ψ ∣ P1,P2 | ⎤
⎦ | . M)⋂
Var(Q) = ∅ |
ou encore
| ∀ ( ξQ/K )∈ s,
( FVξK(M) ∖ (Var(P1) ⋃ Var(P2)
⋃ {ψ}))⋂ Var(Q) = ∅
|
et donc par
(R1)
nous obtenons:
|
| | ∀ ( ξQ/K )∈ s
FVξK(M) ⋂ Var(Q) | = |
∅
| (4.1) |
|
- λ [ψ ∣ P1,P2 ]. M est acceptable, ce
que l'on peut reformuler par:
|
| | ∀ | ⎡
⎣ | ξ ∣ Q1,Q2 | ⎤
⎦ | ∈ | ⎡
⎣ | ψ ∣ P1,P2 | ⎤
⎦ | , FVξR(M)⋂
Var(Q1) |
| = |
∅ | (4.2) |
| ∀ | ⎡
⎣ | ξ ∣ Q1,Q2 | ⎤
⎦ | ∈ | ⎡
⎣ | ψ ∣ P1,P2 | ⎤
⎦ | , FVξL(M)⋂
Var(Q2) |
| = | ∅
| (4.3) |
|
Ces quatre remarques étant faites nous allons maintenant pouvoir
montrer que le terme e
'= (λ P1. M) [ ( ψP2/L ).s ] N
est un terme acceptable.Puisque N est acceptable, il nous suffit de montrer que
(λ P1. M) [ ( ψP2/L ).s ]
est acceptable, c'est à dire:
-
∀ ( ξQ/K )∈
( ψP2/L ).s,
FVξK(λ P1. M)∩ Var(Q)=∅.
Soit
( ξQ/K )∈( ψP2/L ).s,
deux cas sont possibles:
-
Si ( ξQ/K )∈ s, il nous faut garantir
que ( FVξK(M) ∖ Var(P1))∩Var(Q)=∅ ce qui est directement déductible de l'équation
(4.1).
- Si ( ξQ/K )=
( ψP2/L ), nous voulons alors montrer que
( FVξL(M) ∖
Var(P1))∩Var(P2)=∅ ce qui est garanti par
l'équation
(4.3).
- λ P1. M est acceptable, ce qui est évident puisque
nous savons:
-
que M est acceptable par (R2),
- et que ∀ [ξ ∣ Q1,Q2 ]∈
P1, FVξR(M)∩ Var(Q1)=∅ et
FVξL(M)∩ Var(Q2) = ∅ par les
équations
(4.2)
et
(4.3).
- Si la règle utilisée est la règle (Abs_right), nous
raisonnons comme dans le cas précédent.
- Si la règle utilisée est la règle (Abs_var), nous savons
alors que e= (λ x. M) [ s ] N et donc que:
- [(R1)]
Les expressions M, s et N sont acceptables.
- ∀ ( ξQ/K )∈
s, FVξK(λ x. M)∩ Var(Q) = ∅
et donc ∀ ( ξQ/K )∈ s,
( FVξK(M)∖ {x})∩ Var(Q)=∅
et donc
| ∀ ( ξQ/K )∈ s, FVξK(M)⋂
Var(Q)=∅ |
puisque par α-conversion nous
pouvons supposer que x∉Var(s).
Il nous faut maintenant montrer que e
'= M [ ( x/N ).s ] est acceptable. A cette fin nous
devons montrer que ( x/N ).s est acceptable, ce que nous
faisons en nous souvenant que, par (R1), N et s sont
acceptables. De même, puisque M est acceptable il nous suffit
de montrer que ∀ ( ξQ/K )∈ ( x/N ).s
FVξK(M)∩ Var(Q) = ∅ ce qui est
exactement (R2).
- Si la règle utilisée est la règle (Abs_wild), le résultat
est immédiat.
- Si la règle utilisée est la règle (Freeze), nous avons
e= [ψ ∣ M,N ] [ s ] d'où nous déduisons que
:
- [(R1)]
s, M et N sont acceptables.
- ∀ ( ξQ/K )∈ s,
FVξK([ψ ∣ M,N ])∩
Var(Q)=∅ ⇔
-
- ∀ ( ξQ/K )∈ s si ξ ≠ψ alors
( FVξK(M) ∪
FVξK(N)∪{ψ})∩ Var(Q) =
∅(1)
- ∀ ( ψQ/L )∈ s,
FVξL(M)∩ Var(Q) = ∅(2)
- ∀ ( ψQ/R )∈ s,
FVξR(N)∩ Var(Q) = ∅(3)
Nous devons maintenant montrer que:
[ ψ [ s ] ∣ s M,N ] est acceptable.
Puisque par (R1) M, N et s sont acceptables il nous suffit
de montrer que:
-
ψ [ s ] est acceptable, ce qui est vrai par
(1) et ce qui implique que:
- Si ψ∉s, nous avons Acc( M [ s ] ) et
Acc( N [ s ] ).
- Si ( ψQ/L )∈ s, nous avons
Acc( M [ s ] ).
- Si ( ψQ/R )∈ s, nous avons
Acc( N [ s ] ).
Ces trois derniers cas sont démontrés aisément par hypothèse d'induction.
- Le résultat est immédiat grâce à la
définition 14 si la règle utilisée est l'une
des suivantes:
| (Left) | (Right) | (Xi) | (app) |
| (left) | (right) | (pair) | (var1) |
| (var2) | (var3) | (var4) | (sum_var1) |
| (sum_var2) | (sum_var3) | (sum_var4) | (id). |
- Si la règle utilisée est la règle (clos), nous avons
alors e= M [ s ] [ t ] d'où nous déduisons que
- [(R1)]
M, s, M [ s ] et t sont acceptables.
- ∀ ( ξQ/K )∈ t,
FVξK( M [ s ] )∩ Var(Q) =
∅.
- ∀ ( ξQ/K )∈ s,
FVξK(M)∩ Var(Q) =
∅.
Nous devons alors montrer que e '= M [ s ∘ t ] est
acceptable c'est à dire:
-
M, s, t sont acceptables ce qui est trivial par (R1).
- s ∘ t est acceptable c'est à dire
| ∀ ( ξQ/K )∈
t, FVξK(s)⋂ Var(Q) = ∅
|
- ∀ ( ξQ/K )∈ s ∘ t,
FVξK(M)∩Var(Q) = ∅
-
Pour démontrer le second point, il nous suffit de remarquer
que
| ∀ K,
FVξK( M [ s ] )=( FVξK(M)
∖ Var(s))⋃ FVξK(s)
|
nous n'avons alors plus qu'à conclure par (R2)
- Pour démontrer le troisième point, il nous suffit de
remarquer que
| ∀ ( ξQ/K )∈
s ∘ t, ( ξQ/K )∈ s ou
( ξQ/K )∈ t |
nous pouvons alors conclure par
(R1)
ou
(R2).
- Si la règle utilisée est la règle (ass_env), nous avons
alors e=(s ∘ t) ∘ u d'où nous déduisons que:
- [(R1)]
Par α-conversion, nous pouvons supposer que
Var(t)∩Var(u)=∅.
- s, t et u sont acceptables.
- ∀ ( ξQ/K )∈
u, FVξK(s ∘ t)∩ Var(Q) =
∅.
- ∀ ( ξQ/K )∈
t, FVξK(s)∩ Var(Q) = ∅.
Nous devons démontrer que s ∘ (t ∘ u) est
acceptable c'est à dire que:
-
s, t et u sont acceptables ce que nous obtenons par
(R2).
- t ∘ u est acceptable c'est à dire ∀
( ξQ/K )∈ u, FVξK(t)∩ Var(Q)
= ∅.
- ∀ ( ξQ/K )∈ t ∘ u,
FVξK(s)∩ Var(Q) = ∅.
-
Le second point est démontré par le fait que:
| FVξK(s ∘ t)=( FVξK(s)∖Var(t))⋃ FVξK(t) |
et par
(R3).
- Le troisième point est démontré par le fait que:
| ∀
( ξQ/K )∈ t ∘ u,
( ξQ/K )∈ t ou
( ξQ/K )∈ u |
et par
(R1).
- Si la règle utilisée est la règle (concat1), nous
avons alors dans ce cas e= (( x/M ).s) ∘ t ce dont
nous déduisons que:
- [(R1)]
M, s et t sont acceptables.
- ∀ ( ξQ/K )∈
t, FVξK(( x/M ).s)∩ Var(Q) = ∅
ou de manière équivalente:
| ∀ ( ξQ/K )∈ t, ( FVξK(M)
⋃ FVξK(s))⋂ Var(Q) = ∅ |
Il nous faut démontrer que e
'=( x/ M [ t ] ).(s ∘ t) est acceptable c'est à dire
que:
-
Les expressions M, s et t sont acceptables ce qui découle
triviallement de (R1).
- Le terme M [ t ] est acceptable ce que nous obtenons
triviallement de (R2) et du fait que FVξK(M)
⊂ FVξK(( x/M ).s).
- s ∘ t pour lequel nous raisonnons comme dans le
cas précédent.
- Si la règle utilisée est la règle (concat2), nous
raisonnons comme dans le cas d'une application de la règle
concat1.
Ce dernier lemme conclut notre définition de λ Pw. Nous n'utiliserons
désormais que des expressions.
Nous allons dans la section suivante montrer que λ Pw est un calcul
confluent sur l'ensemble des expressions.
4.2 Confluence de λ Pw
Cette section est consacrée à l'étude de la confluence de λ Pw. Nous
allons utiliser pour cela une méthode utilisée pour la confluence de
λσ w [CHL96]. Dans un premier temps, nous allons
montrer que la relation →es est confluente et fortement
normalisante. Nous définirons alors une nouvelle relation →λ Pwi
agissant dans l'ensemble des formes normales de →es . Puis nous
montrerons la confluence de →λ Pwi . Nous conclurons enfin à la
confluence de →λ Pw par un lemme technique.
4.2.1 Confluence et terminaison de →es
La preuve de forte normalisation de →es est une preuve par
interprétation. Cette interprétation nous a été fournie par
CiME [CMMU00].
Lemme 21 (Forte normalisation de →es )
La relation →es est fortement normalisante sur l'ensemble des
expressions du calcul λ Pw.
-
- Preuve.
Il suffit de remarquer que si nous considérons la fonction
I() définie ci-dessous et que nous considérons l'ordre
strict >es sur les termes défini par t1>es t2
⇔ I(t1)>I(t2) alors cet ordre est strictement
décroissant sur les règles de →es
| I( L) | = | 0 |
| I( R) | = | 0 |
| I( id) | = | 1 |
| I( x) | = | 0 |
| I( ξ) | = | 0 |
| I( ( x/M ).s) | = | I(M) + I(s) + 1 |
| I( ( ξ/K ).s) | = | I(s) + 1 |
| I( s ∘ t) | = | I(s)* I(t) + I(t) +
3*I(s) + 1 |
| I( ξ [ s ] ) | = | I(s) |
| I( M [ s ] ) | = | I(M)*I(s) + I(s) +
3*I(M) + 1 |
| I( inl (M)) | = | I(M) + 1 |
| I( inr (M)) | = | I(M) + 1 |
| I( ⟨ M1, M2 ⟩) | = | I(M1) + I(M2) + 1 |
| I( M1 M2) | = | I(M1) + I(M2) + 1 |
| I( [ξ ∣ M1,M2 ]) | = | I(M1) + I(M2) + 2 |
| |
| I( [Ξ ∣ s M1,M2 ]) | = | | I(s)*(I(M1) +
I(M2) + 2) + 3*I(M2) |
| + I(Ξ) +
3*I(M1) + 5 |
| |
|
| I() |
Ayant désormais montré que →es est fortement normalisable, nous
allons maintenant nous attacher à démontrer que →es est une
relation confluente. Nous aurons pour cela besoin du lemme suivant:
Lemme 22
Soient s et t deux substitutions et ξ une variable de
choix.
-
Si ξ [ s ] —→*es ξ alors
ξ [ s ∘ t ] —→*es ξ [ t ] .
- Si ξ [ s ] —→*es K alors
ξ [ s ∘ t ] —→*es K.
-
- Preuve.
Nous prouvons ces deux propositions par induction sur la structure
de s puis par cas sur ses réduits en un pas.
-
Si s=id, le résultat est immédiat grâce à la règle
(id) pour le point 1. Le point 2 ne
peut avoir lieu.
- Si s=( x/M ).s1, il est évident que si
ξ [ s ] —→*es T, alors
ξ [ s1 ] —→*es T. Remarquons maintenant que nous
avons
ξ [ s ∘ t ] →es ξ [ ( x/ M [ t ] ).(s1 ∘ t) ] →es ξ [ s1 ∘ t ] .
Nous concluons alors dans les deux cas par hypothèse d'induction.
- Si s=( ψ/K' ).s, deux cas sont
possibles:
-
Si ψ≠ξ nous raisonnons comme dans le cas
précédent.
- Si ψ=ξ, nous ne pouvons bien évidement
qu'être dans le second cas et nous devons avoir K=K'.
D'où
ξ [ s ∘ t ] →es ξ [ ( ξ/K ).(s1 ∘ t) ] →es K
- Si s=s1 ∘ s2, nous commençons par remarquer que
ξ [ s ∘ t ] →es
ξ [ s1 ∘ (s2 ∘ t) ] . Nous
raisonnons alors différemment suivant les cas où nous nous
trouvons:
-
Si ξ [ s ] —→*es ξ nous devons bien
évidement avoir ξ [ s1 ] —→*es ξ et
ξ [ s2 ] —→*es ξ. Nous pouvons alors
appliquer l'hypothèse d'induction à s1 pour obtenir
ξ [ s1 ∘ (s2 ∘ t) ] —→*es ξ [ s2 ∘ t ]
. Pour conclure il nous suffit alors d'appliquer l'hypothèse d'induction à
s2.
- Si ξ [ s ] —→*es K, il est évident que soit
ξ [ s1 ] —→*es K soit
ξ [ s1 ] —→*es ξ et
ξ [ s2 ] —→*es K. Nous pouvons alors conclure
comme dans le cas précédent par hypothèse d'induction.
Grâce au lemme 22, nous
sommes en mesure de démontrer la confluence locale de →es .
Lemme 23
La relation →es est localement confluente.
-
- Preuve.
Toutes les paires critiques de →es sont joignables en un ou
deux pas sauf celle obtenue par l'application au terme
M= [ξ ∣ M1,M2 ] [ s ] [ t ] d'une part de la règle
(Freeze) conduisant au terme
[ ξ [ s ] ∣ s M1,M2 ] [ t ] et
d'autre part de la règle (clos) conduisant au terme
[ξ ∣ M1,M2 ] [ s ∘ t ] . Nous allons raisonner
par cas:
-
Si ξ [ s ] —→*es ξ, nous avons alors les
dérivations suivantes:
| | | | ⎡
⎣ | ξ [ s ] ∣ s M1,M2 | ⎤
⎦ | [ t ] |
| —→*es | | →es |
| | ⎡
⎣ | ξ ∣ M1 [ s ] , M2 [ s ] | ⎤
⎦ | [ t ] |
| →es | ⎡
⎣ | ξ [ t ] ∣ t M1 [ s ] , M2 [ s ] | ⎤
⎦ |
|
|
Il nous faut de nouveau distinguer trois cas:
-
Si ξ [ t ] —→*es ξ nous avons alors:
| | | | ⎡
⎣ | ξ [ t ] ∣ t M1 [ s ] , M2 [ s ] | ⎤
⎦ |
| —→*es | ⎡
⎣ | ξ ∣ t M1 [ s ] , M2 [ s ] | ⎤
⎦ |
| →es |
| | ⎡
⎣ | ξ ∣ M1 [ s ] [ t ] , M2 [ s ] [ t ] | ⎤
⎦ |
| —→*es | ⎡
⎣ | ξ ∣ M1 [ s ∘ t ] , M2 [ s ∘ t ] | ⎤
⎦ |
|
|
Par le lemme 22, nous
obtenons ξ [ s ∘ t ] —→*es ξ et
donc:
| | | | ⎡
⎣ | ξ ∣ M1,M2 | ⎤
⎦ | [ s ∘ t ] |
| →es | | | ⎡
⎣ | ξ [ s ∘ t ] ∣ s ∘ t M1,M2 | ⎤
⎦ |
| —→*es |
| →es | | | ⎡
⎣ | ξ ∣ M1 [ s ∘ t ] , M2 [ s ∘ t ] | ⎤
⎦ |
|
|
- Si ξ [ t ] —→*es L , nous avons alors:
| | | | ⎡
⎣ | ξ [ t ] ∣ t M1 [ s ] , M2 [ s ] | ⎤
⎦ |
| —→*es | ⎡
⎣ | L ∣ t M1 [ s ] , M2 [ s ] | ⎤
⎦ |
| →es |
| M1 [ s ] [ t ] | —→*es | M1 [ s ∘ t ] |
|
Par le lemme 22, nous
obtenons ξ [ s ∘ t ] —→*es L et donc:
| | | | ⎡
⎣ | ξ ∣ M1,M2 | ⎤
⎦ | [ s ∘ t ] |
| →es | | | ⎡
⎣ | ξ [ s ∘ t ] ∣ s ∘ t M1,M2 | ⎤
⎦ |
| —→*es |
| →es | M1 [ s ∘ t ] |
|
- Si ξ [ t ] —→*es R , nous raisonnons comme
dans le cas où ξ [ t ] —→*es L .
Nous avons donc clos le diagramme dans le cas où
ξ [ s ] —→*es ξ.
- Si ξ [ s ] —→*es L, nous avons alors les
dérivations suivantes:
| | | | ⎡
⎣ | ξ [ s ] ∣ s M1,M2 | ⎤
⎦ | [ t ] |
| —→*es | | →es |
| M1 [ s ] [ t ] | →es | M1 [ s ∘ t ] |
|
Par le lemme 22, nous
savons que ξ [ s ∘ t ] —→*es L et donc:
| | | | ⎡
⎣ | ξ ∣ M1,M2 | ⎤
⎦ | [ s ∘ t ] |
| →es | ⎡
⎣ | ξ [ s ∘ t ] ∣ s ∘ t M1,M2 | ⎤
⎦ |
| —→*es |
| →es | M1 [ s ∘ t ] |
|
Nous avons donc clos le diagramme dans le cas où
ξ [ s ] —→*es L. - Si ξ [ s ] —→*es R, nous raisonnons comme
dans le cas où ξ [ s ] —→*es L.
Théorème 24
La relation de réduction →es est fortement normalisable et
confluente.
-
- Preuve.
La preuve de ce théorème est déductible des
lemmes 21,
22 et du lemme de Newman
(lemme 11).
Notation 25
Nous utiliserons désormais la notation ES(e) pour dénoter
l'unique forme normale pour la relation →es (ou es-forme
normale) de l'expression e.
Remarque 26
Nous remarquons que:
-
Si s est une substitution qui est une es-forme normale alors
s ne contient pas le constructeur Concaténation.
- Si le terme M [ s ] est en es-forme normale alors
M=λ P. N avec N en es-forme normale et s en es-forme
normale.
Nous allons maintenant définir la relation →λ Pwi et montrer que
cette relation est confluente.
4.2.2 Définition et confluence de la relation →λ Pwi
Définition 27
Nous définissons la relation →λ Pwi sur les es-formes normales
comme suit. Soient e1 et e2 deux es-formes normales, on dit
que e1 se réduit vers e2 par la réduction →λ Pwi si et
seulement si il existe une expression e1' telle que: e1→P
e1' et ES(e1')=e2.
On peut considérer la relation →λ Pwi comme une relation de
réécriture fondée sur λ Pw mais traitant de manière implicite le
mécanisme de la substitution.
Ainsi par exemple, nous aurons la séquence de réduction suivante dans
le λ Pw-calcul (si N est en es-forme normale):
|
(λ x. x) [ id ] N | →λ Pw | x [ ( x/N ).id ] |
et donc la séquence suivante dans le λ Pwi-calcul:
| (λ x. x) [ id ] N | →λ Pwi | N |
puisque ES( x [ ( x/N ).id ] )=N.
Pour démontrer la propriété de confluence pour →λ Pwi , nous allons
utiliser une technique due à Tait et Martin-Löf [Bar84].
Pour cela nous allons tout d'abord définir une nouvelle relation
>>>.
Nous montrerons alors que →λ Pwi ⊂>>> et que
>>>*⊂—→*λ Pwi . Puis nous montrerons que la relation
>>>* possède la propriété du diamant (c.f.
définition 9) avant de déduire des points
précédents que la relation →λ Pwi est confluente.
Définition 28
La relation >>> est définie sur les es-formes normales
comme étant la plus petite relation réflexive telle que:
| M >>> M' N>>>
N' |
|
| λ P. M N >>> (λ P. M) [ id ] N |
|
| M>>> M' N1>>> N1'
N2>>> N2' s>>>
s' |
|
| (λ ⟨ P1, P2 ⟩. M) [ s ] ⟨ N1, N2 ⟩ >>> ( (λ P1. λ P2. M') [ s' ] N1') N2' |
|
| M>>> M' N>>> N'
s>>>
s' |
|
| (λ @(P1,P2). M) [ s ] N >>> ( (λ P1. λ P2. M') [ s' ] N') N' |
|
| M>>> M' N>>> N'
s>>>
s' |
|
| (λ [ξ ∣ P1,P2 ]. M) [ s ] inl (N) >>> (λ P1. M') [ ( ξP2/L ).s' ] N' |
|
| M>>> M' N>>> N'
s>>>
s' |
|
| (λ [ξ ∣ P1,P2 ]. M) [ s ] inr (N) >>> (λ P2. M') [ ( ξP1/R ).s' ] N' |
|
| M>>> M' N>>> N'
s>>>
s' |
|
| (λ x. M) [ s ] N >>> ES( M' [ ( x/N' ).s' ] ) |
|
| M>>> M' N>>> N'
s>>>
s' |
|
| (λ _ . M) [ s ] N >>> ES( M' [ s' ] )
|
|
| M>>> M' N>>> N' |
|
| ⟨ M, N ⟩>>>⟨ M', N' ⟩ |
|
|
|
|
|
| M>>> M' N>>> N' |
|
| [ξ ∣ M,N ]>>>[ξ ∣ M',N' ] |
|
| M>>> M' s>>>
s' |
|
| ( x/M ).s>>>( x/M' ).s' |
|
| s>>>
s' |
|
| ( ξP/K ).s>>>( ξP/K ).s' |
|
Remarque 29
Nous remarquons que si s et s' sont deux substitutions telles
que s>>> s', alors pour toute variable de choix
ξ, ES( ξ [ s ] )=ES( ξ [ s' ] ). Cette remarque étant faite, nous pouvons démontrer:
Lemme 30 (Compatibilité entre >>> et ES)
Soient s et s' deux substitutions telles que s>>> s'.
-
Pour tous termes M et M' tels que M>>>
M', nous avons
ES( M [ s ] )>>>ES( M' [ s' ] ).
- Pour tout couple de substitutions t et t' tel que
t>>> t', nous avons
ES(t ∘ s)>>>ES(t' ∘ s').
-
- Preuve.
Nous prouvons ces deux propositions en même temps par induction sur
l'ordre lexicographique induit par la structure M ou t pour sa
première composante et par la structure de s pour sa seconde
composante. Nous remarquons de plus que, par définition de
>>>, les expressions M, M', t, t', s et s'
sont des es-formes normales et donc ces six expressions sont égales
à leur es-formes normales.
-
Si M=x et s=id, nous avons alors obligatoirement M'=x et
s'=id et donc:
| ES( M [ s ] )=x>>> x=ES( M' [ s' ] )
|
- Si t=id et s=id nous raisonnons comme dans le cas
précédent.
- Si M=x et s=( x/N ).s1, nous avons alors M'=x et
s'=( x/N' ).s1' avec N>>> N' et
s1>>> s1'. Nous concluons alors par:
| ES( x [ ( x/N ).s1 ] )=N>>>
N'=ES( x [ ( x/N' ).s1' ] )
|
- Si M=y et s=( x/N ).s1 avec x≠ y, nous avons
alors M'=y et s'=( x/N' ).s1' avec N>>> N' et
s1>>> s1'. Nous remarquons que
ES( y [ ( x/N ).s1 ] )=ES( y [ s1 ] ) et
ES( y [ ( x/N' ).s1' ] )=ES( y [ s1' ] ). Nous
concluons alors par hypothèse d'induction.
- Si M=x et s=( ξP/K ).s1 nous avons
alors M'=x et s'=( ξP/K ).s1'
s1>>> s1'. Nous remarquons que:
| ES( x [ ( ξP/K ).s1 ] )=ES( x [ s1 ] )
et
ES( x [ ( ξP/K ).s1' ] )=ES( x [ s1' ] )
|
Nous concluons alors par hypothèse d'induction.
- Si M= (λ P. N) [ u ] , nous avons alors
M'= (λ P. N') [ u' ] avec N>>> N' et
u>>> u'. Nous remarquons alors que
| | | ES( (λ P. N) [ u ] [ s ] )= (λ P. N) [ ES(u ∘ s) ] |
| et |
| ES( (λ P. N') [ u' ] [ s' ] )= (λ P. N') [ ES(u' ∘ s') ] |
|
Nous obtenons par hypothèse d'induction,
ES(u ∘ s)>>>ES(u' ∘ s') ce qui nous
permet de conclure par définition de >>>.
- Si M= M1 M2 et M'= M1' M2' avec
M1>>> M1' et M2>>> M2', il nous suffit
de remarquer que
ES( ( M1 M2) [ s ] )= ES( M1 [ s ] ) ES( M1 [ s ] )
(de même pour M'). Par hypothèse d'induction, nous savons que
ES( M1 [ s ] )>>>ES( M1' [ s ] ) et
ES( M2 [ s ] )>>>ES( M2' [ s ] ). Nous
concluons alors par définition de >>>.
- Si M= (λ P. M1) [ u ] N avec
P≠ _ et P≠ x nous raisonnons comme dans le cas
précédent.
- Si M= (λ x. M1) [ u ] N et
M'=ES( M1' [ ( x/N' ).u' ] ) avec M1>>>
M1', N>>> N' et u>>> u', nous remarquons
alors que:
| | | ES( ( (λ x. M1) [ u ] N) [ s ] ) | = | ES( (λ x. M1) [ ES(u ∘ s) ] ES( N [ s ] )) |
| | et | |
| ES( M1' [ ( x/N' ).u' ] [ s' ] ) | = | ES( M1' [ ( x/ES( N' [ s' ] ) ).ES(u' ∘ s') ] ) |
|
Par hypothèse d'induction, nous savons que
ES(u ∘ s)>>>ES(u' ∘ s') et
ES( N [ s ] )>>>ES( N' [ s' ] ) . Nous
concluons alors par définition de >>>.
- Si M= (λ _ . M1) [ u ] N et
M'=ES( M1' [ u' ] ) avec M1>>> M1', et
u>>> u', nous raisonnons comme dans le cas précédent.
- Si [ξ ∣ M1,M2 ] et M'=[ξ ∣ M1',M2' ] avec
M1>>> M1' et M2>>> M2', nous étudions de
manière indépendante les deux sous cas possibles:
-
Si ES( ξ [ s ] )=ξ, nous avons alors:
| ES( | ⎡
⎣ | ξ ∣ M1,M2 | ⎤
⎦ | [ s ] )= | ⎡
⎣ | ξ ∣ ES( M1 [ s ] ),ES( M2 [ s ] ) | ⎤
⎦ |
Nous savons, par hypothèse d'induction, que:
| | | ES( M1 [ s ] )>>>ES( M1' [ s' ] ) | et | ES( M2 [ s ] )>>>ES( M2' [ s' ] ) |
|
Par la
remarque 29,
nous savons que ES( ξ [ s' ] )=ξ. Nous
concluons alors par définition de >>>.
- Si ES( ξ [ s ] )=L (resp.
ES( ξ [ s ] )=R) il nous suffit alors de remarquer
que, dans ce cas, ES( [ξ ∣ M1,M2 ] [ s ] )=ES( M1 [ s ] )
(resp. ES( [ξ ∣ M1,M2 ] [ s ] )=ES( M2 [ s ] )
) pour pouvoir conclure par hypothèse d'induction.
- Si t=( x/M ).t1, nous raisonnons comme dans le cas
d'une application.
- Si t=( ξ/K ).t1, le résultat est évident.
- Il n'y a pas d'autre cas puisque ni
[Ξ ∣ s M1,M2 ], ni M1 [ t ] dans le cas où
M1≠λ P. M, ni t1 ∘ t2 ne sont des
es-formes normales.
Grâce au lemme précédent, nous sommes en mesure de démontrer que
>>> possède la propriété du diamant.
Lemme 31
Le système de réécriture >>> possède la propriété de
forte confluence où de manière équivalente:Si les expressions e, e1 et e2 sont de es-formes normales
telles que: e>>> e1 et e>>> e2, alors il
existe une expression e ' telle que e1>>> e ' et
e2>>> e '.
-
- Preuve.
La preuve de ce lemme est obtenue par induction sur la structure de
l'expression e. Nous démontrons ici uniquement les deux cas qui
ne sont pas évidents pas hypothèse d'induction.
-
Si e= (λ x. M1) [ s ] N et si l'un au
moins des deux réduits (nous supposerons ici que ce réduit est
e1) est un "bêta réduit" de e. Nous avons donc
e1=ES( M1' [ ( x/N1' ).s' ] ) où M1>>>
M1', N1>>> N1' et s>>> s'. Deux cas sont
possibles:
-
Si e2= (λ x. M1'') [ s'' ] N'' où
M1>>> M1'', N1>>> N1'' et
s>>> s'' alors, par hypothèse d'induction, il existe M1''', N'''
et s''' tels que:
| M1'>>> M1''' | , | M1''>>> M1''' |
| N'>>> N''' | , | N''>>> N''' |
| s'>>> s''' | , | s''>>> s''' |
Par définition de >>>, nous avons donc
e2>>>ES( M1''' [ ( x/N1''' ).s''' ] )=e'.
D'autre part nous obtenons, par le
lemme 30,
( x/N1' ).s'>>>( x/N1''' ).s''' dans un
premier temps puis enfin e1>>> e'.
- Pour le cas où e2 est aussi un "bêta réduit" de e nous
utilisons l'hypothèse d'induction et le
lemme 30.
- Si e= (λ _ . M1) [ s ] N et si l'un
au moins des deux réduits est un "bêta réduit" de e, nous
pouvons raisonner comme dans le cas précédent.
Nous déduisons de ce dernier lemme et du lemme de Newman 11 la confluence
de la relation >>>.
Corollaire 32
La relation >>> est confluente.
D'où nous déduisons la confluence de →λ Pwi .
Lemme 33
La relation de réduction →λ Pwi est confluente.
-
- Preuve.
Nous remarquons tout d'abord que nous avons trivialement
→λ Pwi ⊆>>>. De même nous avons
>>>⊂—→*λ Pwi et donc —→*λ Pwi =>>>* .
Nous obtenons alors le résultat par le
corollaire 32.
4.2.3 Confluence de →λ Pw
Afin de pouvoir déduire de ce qui précède la confluence de →λ Pw ,
nous avons besoin d'un certain nombre de lemmes techniques.
Lemme 34
Soient e et e ' deux expressions. Si e→P e ' alors
ES(e)—→*λ Pwi ES(e ').
-
- Preuve.
Nous raisonnons par induction sur (νσ(e),e) où νσ(e)
est la longueur de la plus longue dérivation de e par la relation
→es .
-
Si e=x, e=ξ ou e=id, le résultat est immédiat
puisque e ne peut avoir de réduit par →P .
- Si la réduction n'a pas lieu en tête, nous obtenons
trivialement le résultat par hypothèse d'induction.
- Si
e= (λ ⟨ P1, P2 ⟩. M) [ s ] ⟨ N1, N2 ⟩
et e '=
( (λ P1. λ P2. M) [ s ] N1) N2,
nous remarquons que:
| | | ES(e) | = | (λ ⟨ P1, P2 ⟩. ES(M)) [ ES(s) ] ⟨ ES(N1), ES(N2) ⟩ |
| | et |
| ES(e ') | = | ( (λ P1. λ P2. ES(M)) [ ES(s) ] ES(N1)) ES(N2) |
|
Il est alors évident que l'on a ES(e)→λ Pwi ES(e ').
- Dans les cas d'une application de l'une des règles
(Abs_contr), (Abs_left) ou (Abs_right) nous raisonnons comme
dans le cas précédent.
- Si e= (λ x. M) [ s ] N et e '=
M [ ( x/N ).s ] , nous remarquons que:
| | | ES(e) | = | (λ x. ES(M)) [ ES(s) ] ES(N) |
| | et |
| ES(e ') | = | ES( ES(M) [ ( x/ES(N) ).ES(s) ] ) |
|
d'où le résultat.
- Si e= (λ _ . M) [ s ] N et e '=
M [ s ] , nous raisonnons comme dans le cas précédent.
Remarque 35
Soient e1 et e2 deux es-formes normales. Si e1→λ Pwi e2,
alors e1—→*λ Pw e2.
Théorème 36 (Confluence de →λ Pw )
La relation →λ Pw est confluente.
-
- Preuve.
Nous utilisons pour faire cette démonstration le
lemme 13 dans lequel nous posons:
-
R=→λ Pw
- R1=→es
- R2=→P
- R'=→λ Pwi
Nous avons bien R= R1∪ R2. De plus par le
théorème 24, R1 est confluente
et fortement normalisable. Nous obtenons R'⊂
R* par le lemme 34 et le
point (2.b) par la remarque 35.
4.3 Un système de types pour λ Pw
Nous allons consacrer cette section à la définition du système de
types associé au λ Pw-calcul et à la preuve de la propriété de
préservation de types par réduction. La définition d'un système de
types pour un formalisme répond à deux attentes. La première de ces
attentes est la cohérence des données. Si par exemple, nous avons
spécifié qu'une fonction attend en argument des entiers naturels, le
système de types nous garantit dès la compilation que les arguments
passés à cette fonction seront bien des entiers et non des chaînes de
caractères ou des réels. Sur un plan plus théorique, les systèmes de
types sont utilisés dans les formalismes dérivant du λ-calcul afin
d'identifier un fragment décidable de leur ensemble d'expressions qui
possède la propriété de normalisation forte. Nous utiliserons quant à
nous le système de types de cette section à cette dernière fin. Le
système de types donné ici est un système de types simples. Il dérive
de ceux des prédécesseurs de λ Pw [KPT96, CK99a]. Ces
calculs fondaient leur système de types sur un isomorphisme de
Curry-Howard fondé sur le calcul des séquents de
Gentzen [Gen69] pour la logique intuitionniste.
4.3.1 Définition du système de dérivation de type
Nous allons dans cette section être amenés à restreindre l'ensemble des
motifs du calculs (et donc des expressions) à l'ensemble des motifs
linéaires compatibles avec un type A. Le rôle de cet ensemble
est de nous assurer par exemple qu'un motif pair est bien associé à
un type produit. La linéarité des motifs nous permettra d'éviter les
motifs compatible avec un type mais mal formés tel que ⟨ x, x ⟩
qui est a priori compatible avec le type A1× A2 mais mal formé
pour ce type.
Définition 37 (Motif compatible)
L'ensemble des motifs compatibles avec un type A noté
COMP(A) est défini comme étant le plus petit ensemble de motifs
linéaires (Définition 3) vérifiant:
| _ | ∈ | COMP(A) |
| x | ∈ | COMP(A) | pour toute variable x |
| @(P,Q) | ∈ | COMP(A) | si P∈ COMP(A) et
Q∈ COMP(A) |
| ⟨ P, Q ⟩ | ∈ | COMP(B× C) | si P∈ COMP(B) et
Q∈ COMP(C) |
| [ξ ∣ P,Q ] | ∈ | COMP(B+ C) | si P∈ COMP(B) et
Q∈ COMP(C) |
A titre d'exemple, le motif ⟨ x, y ⟩ est linéaire mais n'est pas
compatible avec le type A + B.
Nous allons maintenant définir les environnements de types.
Définition 38 (Environnement de types)
Un environnement de types est une paire Φ ;Γ telle que:
-
Φ, appelé environnement de variables de choix, est un
ensemble de couple ξ : K,
- et Γ, appelé
environnement de motifs, est un ensemble de couple P : A.
Un environnement de types est dit linéaire si toute variable
(usuelle ou de choix) n'apparaît au plus qu'une fois dans cet
environnement.
Un environnement de types Φ;Γ est dit
compatible si et
seulement si pour tout couple P : A dans Γ, P∈ COMP(A).
Nous étendons de manière naturelle les notions de variables liées par
un motif
(Definition 8) aux environnements de types.
Nous allons maintenant donner les règles de dérivation de type pour le
système λ Pw.
Définition 39 (Règle de dérivation de type)
Les règles de dérivation de type du λ Pw-calcul sont données
ci-dessous. Ces règles utilisent les notations déjà introduites au
chapitre 3 d'une part et une nouvelle notation
↝ qui nous servira à informellement à savoir si un choix a
été fait sur une variable de choix ξ.
| Les termes |
| |
| |
|
| Φ;x1 : A1,…,xn : An
⊢ xi : Ai |
(Proj1) |
| |
| Φ;Γ⊢ M :
A |
|
| Φ;Γ⊢ inlB(M) : A+B |
(+Right1) |
| |
| Φ;Γ⊢ M : B |
|
| Φ;Γ⊢
inrA(M) : A+B |
(+Right2) |
| |
| Φ;Γ⊢ ξ ↝ ξ |
| Φ;P : B,Γ⊢ M : A |
| Φ;Q : C,Γ⊢
N : A |
|
|
| Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ [ξ ∣ M,N ] :
A |
(Case1) |
| |
| Φ;Γ⊢ ξ ↝ K
Φ;Γ⊢ M : A Φ;Γ⊢ N : A |
|
|
Φ;Γ⊢ [ξ ∣ M,N ] : A |
(Case2) |
| |
| Φ;Γ⊢Ξ ↝ ξ |
| Φ;P : A,Γ⊢ M [ s ] : C |
| Φ;Q :
B,Γ⊢ N [ s ] : C |
|
|
| Φ;[ξ ∣ P,Q ] :
A+B,Γ⊢[Ξ ∣ s M,N ] : C |
(Frozencase1) |
| |
| Φ;Γ⊢Ξ ↝ K |
| Φ;Γ⊢ M [ s ] : A |
| Φ;Γ⊢ N [ s ] : A |
|
|
|
Φ;Γ⊢[Ξ ∣ s M,N ] : A |
(Frozencase2) |
| |
| Φ;P : A, Q : B,Γ⊢ M :
C |
|
| Φ;⟨ P, Q ⟩ : A× B,Γ⊢
M : C |
(× Left) |
| |
| Φ;Γ⊢ M :
A Φ;Γ⊢ N :
B |
|
| Φ;Γ⊢⟨ M, N ⟩ : A× B |
(× Right) |
| |
| Φ;P : A,Γ⊢ M :
B |
|
| Φ;Γ⊢λ P : A. M : A→ B |
(→ Right) |
| |
| Φ;Γ⊢ M : A→ B
Φ;Γ⊢ N : A |
|
| Φ;Γ⊢
( M N) : B |
(App) |
| |
| Φ;P : A,Q : A,Γ⊢ M :
B |
|
| Φ;@(P,Q) : A,Γ⊢ M : B |
(Layered) |
| |
| Φ;Γ⊢ M : B |
|
| Φ;P :
A,Γ⊢ M : B |
(Wildcard) |
| |
| |
| Les substitutions |
| |
|
(axiom) |
| |
| Φ;Γ⊢ t ▷
Φ';Γ ' Φ';Γ '⊢ s ▷ Φ'';Γ
'' |
|
| Φ;Γ⊢s ∘ t ▷ Φ'';Γ '' |
(concat) |
| |
| Φ;Γ⊢ M : A
Φ;Γ⊢ s ▷ Φ';Γ
' |
|
| Φ;Γ⊢( x/M ).s ▷ Φ';x:A,Γ ' |
(cons1) |
| |
| Φ;Γ⊢
s ▷ Φ';Γ ' |
|
| Φ;Γ⊢( ξP :
A/K ).s ▷ ξ : K,Φ';P : A,Γ ' |
(cons2) |
| |
| Φ;Γ⊢ s ▷ Φ';Γ
' Φ';Γ '⊢ M :
A |
|
| Φ;Γ⊢ M [ s ] : A |
(term) |
| |
| |
| Les termes de choix |
| |
| |
|
| ξ1 : K1,…,ξm :
Km;Γ ⊢ ξj ↝ Kj |
(Proj2) |
| |
| si ∀ i,ξ≠ξi |
|
| ξ1 : K1,…,ξm : Km;Γ
⊢ξ ↝ ξ |
(Nproj) |
| |
|
(L) |
| |
|
(R) |
| |
| Φ;Γ⊢ s ▷ Φ';Γ
' Φ';Γ'⊢
ξ ↝ T |
|
| Φ;Γ⊢ ξ [ s ] ↝ T |
(sum) |
-
Dans les règles précédentes tous les environnements sont
supposés linéaires et compatibles. De même tout les motifs sont
supposés linéaires et compatibles avec les types qui leur sont
associés.
- Dans les règles
(Case1) et (Frozencase1), la variable de choix
ξ est supposée être une variable
fraîche.
- Les variables ξi des règles (Nproj) et (Proj2)
sont deux à deux distinctes.
- La variable ξ de la règle (Nproj) n'apparaît pas dans
Γ.
- Le terme N apparaissant dans la règle (App) ne
contient pas de variable de choix libre.
- La substitution s apparaissant dans les règles (term),
(Frozencase1) et (Case1) ne contient pas de variable de
choix libre.
- Le terme M de la règle (cons1) ne contient pas de
variable de choix libre.
Enfin nous dirons que le terme M (resp. la substitution s ou le
terme de choix Ξ) possède le type A (resp. le
co-environnement Φ';Γ' ou le type de choix T)
dans l'environnement Φ;Γ si et seulement si il
existe une dérivation de types se terminant par
Φ;Γ⊢ M : A (resp.
Φ;Γ⊢ s ▷ Φ';Γ' ou
Φ;Γ⊢ Ξ ↝ T). Nous dirons que
le terme M (resp. la substitution s ou le terme de choix
Ξ) est bien typé dans l'environnement
Φ;Γ si et seulement si il existe un type A
(resp. un co-environnement Φ';Γ' ou un type de
choix T) tel que M possède le type A (resp. s possède le
co-environnement Φ';Γ', Ξ possède le
type de choix T) dans Φ;Γ. Nous ferons dans
la suite un abus de notation en notant Φ;Γ⊢
M : A (resp. Φ;Γ⊢ s ▷
Φ';Γ' ou Φ;Γ⊢ Ξ
↝ T) pour dénoter le fait que le terme M (resp. la
substitution s ou le terme de choix Ξ) possède le
type A (resp. le co-environnement Φ';Γ' ou le
type de choix T) dans l'environnement Φ;Γ.
De même, il nous arrivera, dans la suite de ce chapitre, d'écrire
qu'une expression est bien typée dans un
environnement de types pour exprimer le fait que cette expression
possède un type dans cet environnement.
Nous commençons par remarquer que:
Remarque 40
Si une substitution s est bien typée dans un environnement
Φ ;Γ , alors pour tout co-environnement Φ ';Γ ' de s
dans Φ ;Γ on a Φ⊂Φ' et Γ⊂Γ'.
Nous remarquons aussi que si e est une expression bien typée dans
Φ;Γ alors toutes ses variables libres apparaissent dans
Φ;Γ.
Le lemme suivant est utilisé dans la preuve de préservation de types
par réduction. Il affirme que si une expression est bien typée dans un
environnement alors cette expression est aussi bien typée dans tout
environnement "raisonnable" contenant cet environnement.
Lemme 41 (Affaiblissement pour les
environnements)
-
Si Φ;Γ ⊢ M : A et
Ψ;Δ est un
environnement linéaire et
compatible, alors si BV(Ψ;Δ)∩
( BV(Φ;Γ)∪ FCV(M) ) =∅ on a
ΨΦ;ΔΓ ⊢ M : A.
- Si Φ;Γ ⊢ s ▷ Φ';Γ', alors pour tout
environnement linéaire et compatible Ψ;Δ tel que
BV(Ψ;Δ)∩ ( BV(Φ';Γ')∪ FCV(M) )
=∅ on a ΨΦ;ΔΓ ⊢
s ▷ ΨΦ';ΔΓ'.
- Si Φ;Γ ⊢ Ξ ↝ T, alors pour tout
environnement linéaire et compatible Ψ;Δ tel que
BV(Ψ;Δ)∩ ( BV(Φ;Γ)∪ FCV(Ξ) )
=∅ on a ΨΦ;ΔΓ ⊢ Ξ ↝ T.
-
- Preuve.
Nous prouvons ce lemme en raisonnant par induction sur l'ordre
lexicographique dont la première composante est la taille ν de
l'environnement de type Ψ;Δ et la seconde composante est la
hauteur h de la preuve connue de chacun des jugements de typage.
Enfin nous raisonnons par cas sur la dernière règle utilisée.
-
Si ν=0 le résultat est immédiat par hypothèse.
- Si la dernière règle est la règle (Proj1), alors M est
une variable et deux cas sont possibles:
-
•
- Si Δ=∅, nous remarquons que par
hypothèse Φ;Γ ne partage pas de variable avec Ψ et
nous concluons en utilisant la règle (Proj1).
- •
- Si Δ=P : B;Δ', alors par hypothèse
d'induction nous savons que ΨΦ;Δ'Γ ⊢ M :
A. Il ne nous reste alors qu'à appliquer la règle
(Wildcard) pour conclure.
- Si la dernière règle est la règle (Proj2), alors Ξ
est une variable de choix et T∈{L,R}. Le résultat
est immédiat en appliquant la règle (Proj2) avec
l'environnement ΨΦ;ΔΓ.
- Si la dernière règle est la règle (Nproj), nous raisonnons
alors comme dans le cas d'une application de la règle
(Proj2).
- Si la dernière règle est la règle (Left) ou la règle
(Right), le résultat est immédiat grâce aux conditions
imposées à Ψ;Δ.
- Si la dernière règle est (+Right1), nous avons
alors M=inlA2(M1) et A=A1+A2. Par hypothèse d'induction nous savons que
ΨΦ;ΔΓ⊢ M1 : A1. Le résultat
est alors obtenu en appliquant la règle (+Right1).
- Si la dernière règle est la règle (cons1), nous savons
alors que s=( x/M ).s1, Φ';Γ'=Φ';x : A,Γ''
et que Φ;Γ⊢ M : A et Φ;Γ⊢ s1 ▷
Φ';Γ'. Nous obtenons alors par hypothèse d'induction que
ΨΦ;ΔΓ⊢ M : A et ΨΦ;ΔΓ⊢
s1 ▷ ΨΦ';ΔΓ' et il ne nous reste plus qu'à
utiliser la règle (cons1) pour pouvoir conclure.
- Si la dernière règle est la règle (cons2), nous
raisonnons comme dans le cas de l'application de la règle
(cons1).
- Les autres cas sont évidents par hypothèse d'induction.
La remarque suivante est utilisée dans la preuve de préservation de
types par réduction.
Remarque 42
Si s est une substitution telle que
Φ;Γ⊢ s ▷
Φ';[ξ ∣ P,Q ] : A+B,Γ' alors s'il existe un terme
M=[ξ ∣ M1,M2 ] ou un terme
M=[ ξ [ u ] ∣ t M1,M2 ] tel
que ξ∉ BV(u) et
M [ s ] soit acceptable alors [ξ ∣ P,Q ] : A+B ∈ Γ.
-
- Preuve.
Supposons que [ξ ∣ P,Q ] : A+B ∉ Γ, nous remarquons alors
par induction sur la structure de s qu' il doit exister une
variable de choix ψ et une constante de choix K tels que
( ψ[ξ ∣ P,Q ]/K )∈ s, nous concluons en utilisant la
remarque 16.
4.3.2 Préservation de types par réduction
Nous allons maintenant nous attacher à la démonstration de la
préservation de types par réduction. Cette démonstration repose sur
deux points clés. La possibilité de "déstructurer" des environnements
de types d'une part et celle de "choisir" la forme d'une dérivation de
typage (sous réserve de l'existance d'une dérivation) d'autre
part.
Définition 43 (Déstructuration de motifs)
Étant donné un motif P compatible avec le type A nous
définissons sa déstructuration, notée Des(P : A), par
induction sur P comme suit:
| | | Des( _ : A) | = | _ : A |
| Des(x : A) | = | x : A |
| Des( | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B) |
| = | |
| Des(⟨ P, Q ⟩ : A× B) | = | Des(P : A)Des(Q : B) |
| Des(@(P,Q) : A) | = | Des(P : A)Des(Q : A) |
| | = |
|
Cette notion est étendue de manière naturelle aux environnements de
motif par Des(P1 : A1,…,Pn :
An)=Des(P1 : A1),…,Des(Pn : An).
Comme nous le souhaitions plus haut, le système de types associé à
λ Pw satisfait la propriété de préservation de types par
déstructuration.
Lemme 44 (Préservation de type par
déstructuration) Soient Φ un
environnement de variable de choix, Γ un environnement de motif
et Γ1Γ2 une partition de Γ (en deux sous ensembles
disjoints). Les propriétés suivantes sont satisfaites:
-
Si M est un terme alors Φ;Γ⊢ M : A si et
seulement si Φ;Γ1Des(Γ2)⊢ M : A.
- Si s est une substitution alors Φ;Γ⊢ s ▷
Φ';ΓΓ' si et seulement si
Φ;Γ'Γ1Des(Γ2)⊢ s ▷
Φ';Γ'Γ1Des(Γ2).
- Si Ξ est un terme de choix alors
Φ;Γ⊢ Ξ ↝ T si et seulement si
Φ;Γ1Des(Γ2)⊢ Ξ ↝ T.
-
- Preuve.
Nous prouvons les trois propriétés ensemble. Nous commençons par la
preuve de l'implication directe puis nous donnerons la preuve de
l'implication réciproque.
La preuve de l'implication directe est obtenue par induction
sur la hauteur h de la preuve P déjà connue, puis par cas
sur la dernière règle de typage utilisée.
-
Si la preuve est de hauteur 0, l'unique règle utilisée est
l'un des axiomes du système de typage. Il suffit alors de
remarquer que Φ;Γ1Des(Γ2) satisfait aussi les
conditions de cet axiome pour conclure.
- Si la dernière règle utilisée est la règle (+Right1), alors
la preuve P se termine comme suit:
|
| | Φ;Γ⊢ M : A |
|
| Φ;Γ⊢inlB(M) : A+B |
|
|
Nous savons qu'il existe une preuve de
Φ;Γ1Des(Γ2)⊢ M : A par
hypothèse d'induction. Nous concluons alors ce cas
en appliquant la règle (+Right1).
- Si la dernière règle utilisée est la règle (+Right2), nous
raisonnons comme dans le cas d'une application de la règle
(+Right1).
- Si la dernière règle utilisée est la règle (Case1), nous
avons alors M=[ξ ∣ M1,M2 ] et nous savons que la preuve
P se termine par:
|
| | Φ;Γ⊢ ξ ↝ ξ Φ;P : B,Γ⊢
M1 : A Φ;Q : C,Γ⊢ M2 : A |
|
| Φ;[ξ ∣ P,Q ] : B+C,Γ⊢[ξ ∣ M1,M2 ] : A |
|
|
Par hypothèse d'induction, nous obtenons des preuves de
Φ;Γ1Des(Γ2)⊢ ξ ↝ ξ,
Φ;P :
B,Γ1Des(Γ2)⊢ M1 : A et Φ;Q :
C,Γ1Des(Γ2)⊢ M2 : A ce qui nous suffit pour
conclure en utilisant ces trois preuves pour la règle (Case1),
puisque par définition de la fonction Des() nous pouvons
supposer que [ξ ∣ M1,M2 ] : B+C ∈ Γ1.
- Si la dernière règle utilisée est la règle (Case2), nous
avons alors M=[ξ ∣ M1,M2 ] et nous savons que la preuve
P se termine par:
|
| | Φ;Γ⊢ ξ ↝ K Φ;Γ⊢ M1 :
A Φ;Γ⊢ M2 : A |
|
| Φ;Γ⊢[ξ ∣ M1,M2 ] : A |
|
|
Par hypothèse d'induction, des preuves de
Φ;Γ1Des(Γ2)⊢ ξ ↝ K,
Φ;Γ1Des(Γ2)⊢ M1 : A et
Φ;Γ1Des(Γ2)⊢ M2 : A existent, ce qui nous suffit
pour conclure en utilisant ces trois preuves pour la règle
(Case2).
- Si la dernière règle utilisée est la règle (Frozencase1),
nous raisonnons comme dans le cas de l'application de la règle
(Case1).
- Si la dernière règle utilisée est la règle (Frozencase2),
nous raisonnons comme dans le cas de l'application de la règle
(Case2).
- Si la dernière règle utilisée est la règle (× Left),
nous savons alors que Γ=⟨ P, Q ⟩ : B× C,Γ' et que la
preuve P se termine par:
|
| | Φ;P : B,Q : C,Γ'⊢ M :
A |
|
| Φ;⟨ P, Q ⟩ : C,Γ'⊢ M : A |
|
|
Deux cas sont alors possibles:
-
Si ⟨ P, Q ⟩ : B× C∈Γ1 alors, par hypothèse d'induction, nous
savons qu'il existe une preuve de Φ;P1 : B,P2 :
C,Γ1'Des(Γ2)⊢ M : A (où
Γ1=⟨ P, Q ⟩ : B× C,Γ1'). Nous concluons alors en
utilisant cette preuve pour la règle (× Left).
- Si ⟨ P, Q ⟩ : B× C∉Γ1, nous concluons alors
par hypothèse d'induction en remarquant que pour tout Δ,
Des(⟨ P, Q ⟩ : B× C,Δ)= Des(P : B,Q :
C,Δ).
- Si la dernière règle utilisée est la règle (Layered), nous
raisonnons comme dans le cas de l'application de la règle
(× Left).
- Si la dernière règle utilisée est la règle (Wildcard),
nous savons alors que Γ=P : B,Γ', et que la preuve
P se termine par:
|
| | Φ;Γ'⊢ M : A |
|
| Φ;P : B,Γ'⊢ M : A |
|
|
De nouveau, deux cas sont possibles:
-
Si P : B∈ Γ1, nous raisonnons comme dans le cas de
l'application de la règle (× Left).
- Si P : B∈Γ2, par hypothèse d'induction, nous avons une preuve de
Φ;Γ1Γ2'⊢ M : A (où Γ2=P : B,Γ2').
Nous concluons en introduisant un à un, grâce à la règle
(Wildcard), tous les motifs présents dans Des(P : B).
- Si la dernière règle utilisée est la règle (cons2),
nous avons alors s=( ξP : A/B ).s1 et, par hypothèse d'induction, nous
obtenons une preuve de Φ;Γ1Des(Γ2)⊢ s1 ▷
Φ'';Γ1Des(Γ2)Γ' où Φ'=ξ : K,Φ''.
Nous concluons alors en appliquant la règle (cons2).
- Les autres cas sont immédiats par hypothèse d'induction.
La partie si de la preuve est obtenue une fois de plus par
induction sur la hauteur de la preuve connue des jugements et en
remarquant qu'il suffit dans ces preuves d'appliquer les règles
(× Left), (Layered) et (Wildcard) pour
"reconstruire" Γ2 à partir de Des(Γ2).
Corollaire 45
Soient Φ ;Γ un environnement de type. Les propriétés suivantes sont satisfaites:
-
Si M est un terme alors Φ;Γ⊢ M : A si et
seulement si Φ;Des(Γ)⊢ M : A.
- Si s est une substitution alors Φ;Γ⊢ s ▷
Φ';ΓΓ' si et seulement si
Φ;Γ'Des(Γ)⊢ s ▷ Φ';Γ'Des(Γ).
- Si Ξ est un terme de choix alors Φ;Γ⊢
Ξ ↝ T si et seulement si Φ;Des(Γ)⊢
Ξ ↝ T.
La preuve de préservation de types par réduction nécessite aussi de
pouvoir, dans certains cas, inverser deux applications de règles dans
une preuve afin de travailler sur une "forme canonique" de règle.
Lemme 46
Soient R et W deux règles de typage appartenant respectivement
aux ensembles
| | | {(× Right), (→ Right), (App), (+Right1),
(+Right2)} |
| et |
| {(× Left),
(Layered), (Wildcard) } |
|
Si le jugement Φ;Γ⊢ M : A possède une preuve
P se terminant par l'application de la règle R puis l'application
de la règle W, il existe alors une preuve du même jugement se
terminant par une application de la règle W puis de la règle R.
-
- Preuve.
La preuve de ce lemme est obtenue grâce à un raisonnement par cas
sur W puis sur R.
-
Si W=(× Left), nous savons alors que
Γ=⟨ P, Q ⟩ : B× C,Γ'. Étudions maintenant les
différents cas pour R.
- [•]
Si R=(+Right1), nous savons que A=A1+A2, et que
M=inlA2(M1) d'où nous déduisons que la preuve P se termine par:
|
|
| Φ;P : B,Q : C,Γ'⊢ M1 :
A1 |
|
| Φ;P : B,Q : C,Γ'⊢ inlA2(M1) :
A1+A2 |
R |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢
inlA2(M1) : A1+A2 |
| W
|
Il est alors évident que nous avons aussi une preuve se
terminant par:
|
|
| Φ;P : B,Q : C,Γ'⊢ M1 :
A1 |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢ M1 :
A1 |
W |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢
inlA2(M1) : A1+A2 |
| R
|
- Si R=(+Right2) nous raisonnons alors comme dans le cas où
R=(+Right1).
- Si R=(× Right), nous savons alors que A=A1× A2 et que
M=⟨ M1, M2 ⟩. De plus la preuve P se termine comme
suit:
|
|
| Φ;P : B,Q : C,Γ'⊢ M1 :
A1 Φ;P : B,Q : C,Γ'⊢ M2 :
A2 |
|
| Φ;P : B,Q : C,Γ'⊢ ⟨ M1, M2 ⟩ :
A1× A2 |
R |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ⊢⟨ M1, M2 ⟩ :
A1× A2 |
| W |
|
|
d'où nous déduisons de manière évidente les preuves suivantes:
|
| | Φ;P : B,Q : C,Γ'⊢ M1 :
A1 |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢ M1 :
A1 |
| W |
|
| et |
|
| | Φ;P : B,Q : C,Γ'⊢ M2 :
A2 |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢ M2 :
A2 |
| W |
|
|
Nous concluons alors en appliquant à ces deux preuves la règle R.
- Si R=(→ Right), nous savons que A=A1→ A2, que
M=λ R : A1. M1 et que la preuve P se termine
comme suit:
|
|
| Φ;P : B,Q : C,R : A1,Γ'⊢
M1 : A2 |
|
| Φ;P : B,Q : C,Γ'⊢ λ R :
A1. M1 : A1→ A2 |
R |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ⊢
λ R : A1. M1 : A1→A2 |
| W
|
d'où nous déduisons la preuve suivante:
|
|
| Φ;P : B,Q : C,R : A1,Γ'⊢
M1 : A2 |
|
| Φ;⟨ P, Q ⟩ : B× C,R : A1Γ'⊢ M1 : A2 |
W |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ⊢
λ R : A1. M1 : A1→A2 |
| R |
|
|
- Si R=(App), nous savons que M= M1 M2 et
que la preuve P se termine par:
|
|
| Φ;P : B,Q : C,Γ'⊢ M1 : D→
A Φ;P : B,Q : C,Γ'⊢ M2 : D |
|
| Φ;P :
B,Q : C,Γ'⊢ M1 M2 : A |
R |
|
| Φ;⟨ P, Q ⟩ :
B× C,Γ⊢ ( M1 M2) : A |
| W |
|
|
d'où nous déduisons les deux preuves suivantes:
|
| | Φ;P : B,Q : C,Γ'⊢ M1 : D→
A |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢ M1 :
D→ A |
| W |
|
| et |
|
| | Φ;P : B,Q : C,Γ'⊢ M2 :
D |
|
| Φ;⟨ P, Q ⟩ : B× C,Γ'⊢ M2 : D |
| W |
|
|
Nous concluons alors en appliquant à ces deux preuves la règle R.
- Si la règle W est la règle (Layered) les preuves sont
similaires à celles du cas où W est la règle (× Left).
- Si la règle W est la règle (Wildcard), nous savons
que Γ=R : D,Γ' . Étudions désormais les différents cas
pour R.
- [•]
Si R=(+Right1), nous savons que A=A1+A2, et que
M=inlA2(M1) d'où nous déduisons que la preuve P se termine par:
|
|
| Φ;Γ'⊢ M1 : A1 |
|
| Φ;Γ'⊢ inlA2(M1) : A1+A2 |
R |
|
| Φ;R :
D,Γ'⊢inlA2(M1) : A1+A2 |
| W
|
d'où nous déduisons la preuve suivante:
|
|
| Φ;Γ'⊢ M1 : A1 |
|
| Φ;R : D,Γ'⊢ M1 : A1 |
W |
|
| Φ;R :
D,Γ'⊢inlA2(M1) : A1+A2 |
| R
|
- Si R=(+Right2) nous raisonnons comme dans le cas où
R=(+Right1).
- Si R=(× Right), nous savons alors que A=A1× A2 et que
M=⟨ M1, M2 ⟩. De plus la preuve P se termine comme
suit:
|
|
| Φ;Γ'⊢ M1 :
A1 Φ;Γ'⊢ M2 :
A2 |
|
| Φ;Γ'⊢ ⟨ M1, M2 ⟩ :
A1× A2 |
R |
|
| Φ;R : D,Γ⊢⟨ M1, M2 ⟩ :
A1× A2 |
| W
|
d'où nous déduisons de manière évidente la preuve suivante:
|
|
| Φ;Γ'⊢ M1 :
A1 |
|
| Φ;R : D,Γ'⊢ M1 :
A1 |
W
| Φ;Γ'⊢ M2 :
A2 |
|
| Φ;R : D,Γ'⊢ M2 :
A2 |
W |
|
| Φ;R : D,Γ⊢⟨ M1, M2 ⟩ :
A1× A2 |
| R
|
- Si R=(→ Right), nous savons que A=A1→ A2, que
M=λ P : A1. M1 et que la preuve P se termine
comme suit:
|
|
| Φ;P : A1,Γ'⊢
M1 : A2 |
|
| Φ;Γ'⊢ λ P :
A1. M1 : A1→ A2 |
R |
|
| Φ;R : D,Γ⊢
λ P : A1. M1 : A1→A2 |
| W
|
d'où nous déduisons la preuve suivante:
|
|
| Φ;P : A1,Γ'⊢
M1 : A2 |
|
| Φ;R : D,P : A1Γ'⊢ M1 :
A2 |
W |
|
| Φ;R : D,Γ⊢
λ P : A1. M1 : A1→A2 |
| R
|
- Si R=(App), nous savons que M= M1 M2 et
que la preuve P se termine par:
|
|
| Φ;Γ'⊢ M1 : D→
A Φ;Γ'⊢ M2 : D |
|
| Φ;Γ'⊢
M1 M2 : A |
R |
|
| Φ;R : D,Γ⊢ ( M1 M2) : A |
| W
|
d'où nous déduisons la preuve suivante:
|
|
| Φ;Γ'⊢ M1 : D→
A |
|
| Φ;R : D,Γ'⊢ M1 : D→ A |
W
| Φ;Γ'⊢ M2 :
D |
|
| Φ;R : D,Γ'⊢ M2 : D |
W |
|
| Φ;R : D,Γ⊢ ( M1 M2) : A |
| R
|
Nous allons maintenant démontrer que nous pouvons choisir la dernière
règle utilisée dans une preuve de jugement de type.
Lemme 47
Soit Φ;Γ un environnement de types. Si
Φ;Γ⊢ M1 M2 : A
(resp. Φ;Γ⊢λ P : A. M : A→B,
Φ;Γ⊢⟨ M1, M2 ⟩ : A× B,
Φ;Γ⊢inlB(M) : A+B ou
Φ;Γ⊢inrA(M) : A+B) possède une preuve P alors il existe
une preuve de ce jugement se terminant par la règle (App)
(resp. (→ Right), (× Right), (+Right1) ou (+Right2)).
-
- Preuve.
Nous ne prouvons ici que le cas Φ;Γ⊢ M1 M2 :
A. Les autres cas sont similaires. Nous raisonnons par induction
sur la hauteur h de la preuve P.
-
Si la hauteur h est égale à 0, le résultat est immédiat
par vacuité.
- Si la dernière règle utilisée dans la preuve P est la
règle (App), le résultat est évident.
- Supposons que la dernière règle W utilisée dans la preuve
P appartienne à l'ensemble {(× Left),
(Layered), (Wildcard) } .
Nous savons alors que la preuve P est de la forme:
Nous remarquons alors que le terme typé dans la preuve Π est
encore le terme M1 M2. Par hypothèse d'induction, nous savons alors
qu'il existe une preuve équivalente à la preuve Π se terminant
par une application de la règle (App). Nous concluons alors
grâce au lemme 46.
Lemme 48
Soit Φ;Γ un environnement de type. Si Φ;Γ⊢
[ξ ∣ M1,M2 ] : A (resp. Φ;Γ⊢
[Ξ ∣ s M1,M2 ] : A ) est prouvable alors
Φ;Des(Γ)⊢ [ξ ∣ M1,M2 ] : A possède une
preuve se terminant par l'application de l'une des règles (Case1)
ou (Case2) (resp. (Frozencase1) ou (Frozencase2)).
-
- Preuve.
Nous ne donnons ici la preuve que du cas où Φ;Γ⊢
[ξ ∣ M1,M2 ] : A est prouvable, l'autre cas étant
similaire.
Nous commençons par remarquer que par le
corollaire 45, nous avons une preuve
P de Φ;Des(Γ)⊢ [ξ ∣ M1,M2 ] :
A. Nous raisonnons alors par récurrence sur la hauteur h de la
preuve P.
-
Par vacuité si h=0.
- Si la dernière règle utilisée dans la preuve P est
la règle (Wildcard), nous savons alors que cette preuve se
termine par:
|
| | Φ;Γ'⊢ [ξ ∣ M1,M2 ] :
A |
|
| Φ;Des(Γ)⊢ [ξ ∣ M1,M2 ] : A |
| (Wildcard)
|
où Des(Γ)=R : B,Γ' et R est le motif introduit
par la règle (Wildcard).
Par hypothèse de récurrence, deux cas sont possibles:
-
S'il existe une preuve de Φ;Γ'⊢ [ξ ∣ M1,M2 ] :
A se terminant par une application de la règle (Case2),
nous avons alors une preuve se terminant par:
|
|
| Φ;Γ'⊢ ξ
↝ K Φ;Γ'⊢ M1 : A Φ;Γ'⊢
M2 : A |
|
| Φ;Γ'⊢ [ξ ∣ M1,M2 ] :
A |
(Case2) |
|
| Φ;Des(Γ)⊢ [ξ ∣ M1,M2 ] : A |
| (Wildcard) |
|
|
Puisque la règle (Wildcard) est applicable, nous pouvons
supposer que les variables de R, n'apparaissent nulle par
ailleurs dans cette preuve. Ainsi le lemme 41
nous permet de conclure.
- S'il existe une preuve de Φ;Γ'⊢ [ξ ∣ M1,M2 ] :
A se terminant par une application de la règle (Case1), la
variable de choix ξ ne peut apparaître dans le motif
R. On peut donc appliquer le lemme 41 pour conclure.
- La dernière règle utilisée dans la preuve P ne peut
être ni la règle (× Left) ni la règle (Layered) puisque par
définition Des(Γ) ne peut contenir de motif produit ou
de contraction.
- Si la dernière règle utilisée dans la preuve P est la
règle (Case1) ou la règle (Case2) le résultat est immédiat.
Lemme 49
Soit Φ;Γ un environnement de types. Si
Φ;Γ⊢ ( x/M ).s ▷ Φ ';Γ ' (resp.
Φ;Γ⊢
( ξP/A ).s ▷ Φ ';Γ ' ou
Φ;Γ⊢ s ∘ t ▷ Φ ';Γ ') est
prouvable alors il existe une preuve de
Φ;Des(Γ)⊢( x/M ).s (resp.
Φ;Des(Γ)⊢ ( ξP/A ).s ou
Φ;Des(Γ)⊢ s ∘ t) se terminant
par l'application de la règle (cons1) (resp. (cons2)
ou (concat)).
-
- Preuve.
Une seule règle est applicable à ces termes.
Lemme 50
Soit Φ;Γ un environnement de types. Si Φ;Γ⊢
M [ s ] : A est prouvable alors il existe une preuve de Φ;Des(Γ)⊢
M [ s ] : A se terminant par l'application de la règle (term).
-
- Preuve.
c.f. lemme 48.
Nous obtenons aussi par une induction triviale:
Remarque 51
Si Φ;Γ⊢ Ξ ↝ ξ alors ξ n'apparaît pas dans
Φ;Γ.
Lemme 52
Si Φ;Γ⊢ Ξ ↝ ξ est prouvable alors ξ : K,Φ;Γ⊢
Ξ ↝ K est aussi prouvable.
-
- Preuve.
Nous raisonnons par induction sur Ξ.
-
Si Ξ=ξ, alors la seule règle de typage applicable est la
règle (Nproj). En particulier, nous savons que ξ
n'apparaît pas dans Φ;Γ. Donc l'environnement
ξ : K,Φ;Γ est linéaire et compatible et nous pouvons
donc lui appliquer la règle (Proj2).
- Si Ξ= ξ [ s ] , la seule règle applicable est la
règle (sum). La preuve de Φ;Γ⊢ Ξ ↝ ξ se
termine donc par:
|
| | Φ;Γ⊢ s ▷
Φ';Γ' Φ';Γ'⊢
ξ ↝ ξ |
|
| Φ;Γ⊢ ξ [ s ] ↝ ξ |
| (sum)
|
Par la remarque 51, nous
savons que ξ n'apparaît pas dans Φ';Γ'. De plus par la
remarque 40, ξ n'apparaît pas
dans Φ;Γ et donc, par le lemme 41, nous
obtenons une preuve de ξ : K,Φ;Γ⊢ s ▷
ξ : K,Φ';Γ'. Le résultat en découle immédiatement.
- Aucun autre cas n'est possible.
Afin de pouvoir montrer la propriété de préservation de types par
réduction dans le cas d'une des règles de réduction (Abs_left) ou
(Abs_right), nous avons besoin des résultats suivants.
Lemme 53
Soit K une constante de choix.
-
Si Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ M : C est prouvable
alors ξ ↝ K,Φ;P : A,Q : B,Γ⊢ M : C est
aussi prouvable.
- Si Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ s ▷ Φ';[ξ ∣ P,Q ] : A+B,Γ' est prouvable
alors ξ ↝ K,Φ;P : A,Q : B,Γ⊢ s ▷ ξ ↝ K,Φ;P : A,Q : B,Γ est
aussi prouvable.
- Si Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ Ξ ↝ T est prouvable
alors ξ ↝ K,Φ;P : A,Q : B,Γ⊢ Ξ ↝ T est
aussi prouvable si T≠ξ.
-
- Preuve.
Nous ne prouvons ici que le cas où K=L, l'autre cas étant
similaire.
Nous raisonnons par induction sur la structure de l'expression à
typer.
-
Si M est une variable x, nous avons alors une preuve de
Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ x : C. Nous
commençons par remarquer que, puisque [ξ ∣ P,Q ] n'est pas une
variable, toute preuve du jugement Φ;[ξ ∣ P,Q ] :
A+B,Des(Γ)⊢ x : C (nous savons qu'une telle
preuve existe par le corollaire 45)
doit se terminer par l'application de la règle (Wildcard).
Nous raisonnons alors par induction sur Des(Γ) pour
montrer qu'il existe une preuve de ce dernier jugement se
terminant par l'introduction de [ξ ∣ P,Q ] : A+B.
-
Le cas où Des(Γ)=∅ est impossible car dans
ce cas il nous faudrait pouvoir trouver une preuve de
Φ;[ξ ∣ P,Q ] : A+B⊢ x : C ce qui est impossible.
- Sinon, nous remarquons que la seule règle de typage applicable à ce
jugement est la règle (Wildcard). Supposons que cette
application introduise le motif R : D. Nous pouvons alors
aisément inverser les deux applications de la règle
(Wildcard) introduisant les motif R et [ξ ∣ P,Q ].
Nous avons donc une preuve de la forme:
|
| | Φ;Des(Γ)⊢ x :
C |
|
| Φ;[ξ ∣ P,Q ] : A+B,Des(Γ)⊢ x : C |
| (Wildcard)
|
Nous savons alors que ξ n'apparaît pas dans
Φ;Des(Γ).
Donc, par le lemme 41, nous savons que
ξ : K,Φ;Γ⊢ x : C et nous concluons en appliquant
deux fois la règle (Wildcard) pour introduire
successivement les motifs P : A et Q : B. Nous obtenons le
résultat final par le corollaire 45.
- Si la substitution s est l'identité alors nous avons une
preuve du jugement Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ id
▷ Φ;[ξ ∣ P,Q ] : A+B,Γ et l'environnement Φ;[ξ ∣ P,Q ] :
A+B,Γ est linéaire et compatible. Nous en déduisons que
l'environnement ξ : K,Φ;P : A,Q : B,Γ est aussi
linéaire compatible et nous concluons en appliquant la règle (id).
- Si le terme de choix Ξ est une constante de choix alors
nous remarquons que la seule manière de prouver le jugement
Φ;[ξ ∣ P,Q ] : A+B,Γ⊢ K ↝ K est d'appliquer la
règle (Left) ou la règle (Right). Nous déduisons le
résultat de la linéarité et de la compatibilité de
Φ;[ξ ∣ P,Q ] : A+B,Γ.
- Si le terme de choix Ξ est une variable de choix nous
raisonnons comme dans le cas où Ξ est une constante de
choix après avoir remarquer que Ξ≠ξ.
- Si M= M1 M2, alors par le
lemme 47, nous avons une
preuve de ce jugement se terminant par:
|
|
| Φ; | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B,Γ⊢ M1 : D→C |
|
| Φ; | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B,Γ⊢ M2 : D |
|
|
|
| Φ;[ξ ∣ P,Q ] :
A+B,Γ⊢ M1 M2 : C |
| (App)
|
Par hypothèse d'induction, il existe des preuves de ξ : K,Φ;P : A,Q :
B,Γ⊢ M1 : D→C et de ξ : K,Φ;P : A,Q :
B,Γ⊢ M2 : >C. Nous concluons alors en appliquant la
règle (App) à ces deux preuves.
- Si M=⟨ M1, M2 ⟩, M=inlC2(M1),
M=inrC1(M1) ou M=λ R : C1. M1, nous raisonnons
comme dans le cas où M= M1 M2.
- Si M= M1 [ s ] , alors par le
lemme 50, nous avons une preuve
de Φ;[ξ ∣ P,Q ] : A+B,Des(Γ)⊢ M [ s ] : C
se terminant comme suit:
|
|
| Φ; | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B,Des(Γ)⊢ s ▷
Φ'; | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B,Γ' |
|
| Φ'; | ⎡
⎣ | ξ ∣ P,Q | ⎤
⎦ | : A+B,Γ'
⊢ M : C |
|
|
|
| Φ;[ξ ∣ P,Q ] : A+B,Des(Γ)⊢ M [ s ] : C |
| (term)
|
Par hypothèse d'induction, nous connaissons deux preuves de ξ : K,Φ;P :
A,Q : A,Des(Γ)⊢ s ▷ ξ : K,Φ';P : A,Q :
B,Γ' et de ξ : K,Φ';P : A,Q : B,Γ' ⊢ M :
C . Nous obtenons donc, en appliquant la règle (term) à ces
deux preuves, une preuve de ξ : K,Φ;P : A,Q :
B,Des(Γ)⊢ M [ s ] : C et nous concluons par
le corollaire 45.
- Si M=[ψ ∣ M1,M2 ], deux cas sont possibles:
-
Si ψ=ξ, par le
lemme 48 et le
corollaire 45, nous avons une preuve
se terminant par:
|
|
| Φ;Des(Γ)⊢ ξ ↝ ξ |
| Φ;P : A,Des(Γ)⊢ M1 : C |
| Φ;Q : B,Des(Γ)⊢ M2 : C |
| |
|
|
| Φ;[ξ ∣ P,Q ] :
A+B,Des(Γ)⊢[ξ ∣ M1,M2 ] : C |
| (Case1)
|
Donc, par le lemme 52,
nous avons une preuve de
ξ : K,Φ;Des(Γ)⊢ ξ ↝ K. Nous obtenons
de plus des preuves pour ξ : K,Φ;Q : B,P :
A,Des(Γ)⊢ M1 : C et ξ : K,Φ;Q :
B,P : A,Des(Γ)⊢ M2 : C par le
lemme 41. Nous obtenons ainsi une preuve de
ξ : K,Φ;Q : B,P : A,Des(Γ)⊢
[ξ ∣ M1,M2 ] : C en appliquant à ces preuves la règle
(Case2). Nous concluons finalement grâce au
corollaire 45.
- Si ψ≠ξ, la preuve est la même que dans le cas ou M= M1 M2.
- Si M = [Ξ ∣ s M1,M2 ], c.f. M = [ξ ∣ M1,M2 ].
- Si s=( x/M ).s1, le résultat est immédiat par hypothèse d'induction.
- Si s=( ψP/A ).s1, le résultat est immédiat par
hypothèse d'induction après avoir remarqué que nous devons avoir ψ≠ξ.
- Si s=s1 ∘ s2, nous obtenons le résultat par le
lemme 49 et par hypothèse d'induction.
- Si Ξ= ψ [ s ] , le résultat est obtenu par hypothèse d'induction.
Lemme 54
-
Si Φ;P : B,Γ⊢ M : A et
FV(M)∩ BV(P)=∅ alors Φ;Γ⊢ M : A.
- Si Φ;P : B,Γ⊢ s ▷ Φ';P : B,Γ' et FV(s)∩ BV(s) alors Φ;Γ⊢ s ▷
Φ';Γ'.
- Si Φ;P : B,Γ⊢ Ξ ↝ K et
FV(Ξ)∩ BV(P)=∅ alors Φ;Γ⊢Ξ ↝ K.
- ξ : K,Φ;Γ⊢ M : A et
ξ∉ FV(M) alors Φ;Γ⊢ M⊢ A.
- ξ : K,Φ;Γ⊢ s ▷ ξ : K,Φ';Γ' et
ξ∉ FV(s) alors Φ;Γ⊢ s ▷ Φ';Γ'.
- ξ : K,Φ;Γ⊢ Ξ ↝ K' et ξ∉ FV(Ξ) alors Φ;Γ⊢Ξ ↝ K'.
-
- Preuve.
Par induction sur la hauteur de la preuve déjà connue.
Lemme 55
-
Si Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ M : A et si
FV(M)∩ BV([ξ ∣ P,Q ])≠∅ alors ξ∈ FV(M).
- Si Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ s Φ ';Γ '
et si
FV(s)∩ BV([ξ ∣ P,Q ])≠∅ alors ξ∈ FV(M).
-
- Preuve.
Nous raisonnons par induction sur M.
-
Si M est une variable x, alors
Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ x : A. Il est
évident que le seul moyen de pouvoir prouver un tel séquent est
d'éliminer le motif de choix [ξ ∣ P,Q ] : B+C à l'aide de la
règle (Wildcard) ce qui implique que
FV(M)∩ BV([ξ ∣ P,Q ])=∅.
- Si M=[ξ ∣ M1,M2 ], le résultat est immédiat.
- Si M=[Ξ ∣ s M1,M2 ] avec
Φ ;Γ ⊢Ξ ↝ ξ, le résultat est alors immédiat
puisque
ξ∈ FV(Ξ)⊂ FV([Ξ ∣ s M1,M2 ]).
- Pour les autres cas, le résultat est immédiat par hypothèse d'induction.
Cette longue suite de lemmes techniques étant démontrée, nous sommes
maintenant en mesure de démontrer la propriété principale de cette
section: la préservation de types par
réduction.
Théorème 56 (Préservation de types par
réduction)
Le calcul λ Pw possède la propriété de préservation de type par
réduction ou plus formellement:
-
Si Φ;Γ⊢ M : A et si M→ M' alors
Φ;Γ⊢ M' : A
- Si Φ;Γ⊢ s ▷ Φ';Γ' et si s→ s'
alors Φ;Γ⊢ s' ▷ Φ';Γ'
- Si Φ;Γ⊢ Ξ ↝ T et si Ξ→ Ξ' alors
Φ;Γ⊢ Ξ' ↝ T
-
- Preuve.
Nous raisonnons par induction sur la structure des expressions. Nous
ne présenterons dans cette preuve que les cas où la réduction
s'effectue en tête de l'expression. Les cas où la réduction
s'effectue à l'intérieur de l'expression étant immédiat par hypothèse d'induction.
-
Si M=x, s=id, Ξ=ξ, Ξ=L ou Ξ=R, le
résultat est immédiat puisque ces expressions n'ont pas de réduit.
- Si s= ( x/M ).s1 ou s=( ξP : A/A ).s1 alors
les réductions s'effectuent obligatoirement à l'intérieur de s.
- Si s=s1 ∘ s2, nous avons alors, puisque la seule
règle à appliquer à une telle substitution est la règle
(concat), une preuve de:
|
| | Φ;Γ⊢
s2 ▷ Φ'';Γ'' Φ'';Γ''⊢ s1 ▷
Φ';Γ' |
|
| Φ;Γ⊢ s1 ∘ s2 ▷ Φ';Γ' |
|
|
Nous avons alors 4 possibilités:
-
Si s1=( x/M ).s1' et si
s1 ∘ s2→ ( x/ M [ s2 ] ).(s1' ∘ s2) alors par le lemme 49 nous avons une preuve de Φ'';Γ''⊢( x/M ).s1 ▷ Φ';Γ' se terminant comme suit:
|
| | Φ'';Γ''⊢ M : A
Φ'';Γ''⊢ s1' ▷
Φ';Γ''' |
|
| Φ'';Γ''⊢
( x/M ).s1' ▷ Φ';x : A,Γ''' |
|
|
où Γ'=x : A,Γ'''. De cette preuve nous déduisons la
preuve suivante:
|
|
| Φ;Γ⊢
s2 ▷ Φ'';Γ'' |
| Φ'';Γ''⊢
M : A |
|
|
| Φ;Γ⊢ M [ s2 ] : A |
| Φ;Γ⊢
s2 ▷ Φ'';Γ'' |
| Φ'';Γ''⊢ s1' ▷ Φ';Γ''' |
|
|
| Φ;Γ⊢s1' ∘ s2 ▷ Φ';Γ''' |
|
|
|
Φ;Γ⊢
( x/ M [ s2 ] ).(s1' ∘ s2) ▷
Φ;x : A,Γ''' |
|
|
Ce qui est bien le résultat attendu.
- Si s1=( ξP : A/K ).s1' et si
s1 ∘ s2→ ( ξP :
A/K ).(s1' ∘ s2) la preuve est la même que dans
le cas 1.
- Si s1=id et si s1 ∘ s2→ s2, le résultat
est immédiat.
- Si s1=u ∘ v et si
(u ∘ v) ∘ s2→ u ∘ (v ∘ s2)
alors par le lemme 49 nous connaissons un
preuve se terminant comme suit:
|
| | Φ'';Γ''⊢ v ▷
Φ''';Γ''' Φ''';Γ'''⊢
u ▷ Φ';Γ' |
|
| Φ'';Γ''⊢u ∘ v ▷ Φ';Γ' |
|
|
d'où nous déduisons la
preuve suivante:
|
|
| Φ;Γ⊢
s2 ▷ Φ'';Γ'' |
| Φ'';Γ''⊢ v ▷ Φ''';Γ''' |
|
|
| Φ;Γ⊢v ∘ s2 ▷
Φ''';Γ''' |
Φ''';Γ'''⊢ u ▷
Φ';Γ' |
|
| Φ;Γ⊢u ∘ (v ∘ s2) ▷
Φ';Γ' |
|
|
Ce qui est le résultat attendu.
- Si Ξ= ξ [ s ] , nous pouvons supposer, par le
corollaire 45,
que Des(Γ)=Γ. De plus, toute preuve doit
obligatoirement se terminer par la règle (sum). Nous avons donc une preuve
de la forme:
|
| | Φ;Γ⊢ s ▷
Φ';Γ' Φ';Γ'⊢ ξ
↝ K |
|
| Φ;Γ⊢ ξ [ s ] ↝ K |
|
|
Nous avons alors 3 possibilités:
-
Si s=( x/M ).t et si
ξ [ s ] → ξ [ t ] alors, par le lemme 49, nous avons de plus une
preuve se terminant par:
|
| | Φ;Γ⊢ M : A
Φ;Γ⊢ t ▷
Φ';Γ'' |
|
| Φ;Γ⊢( x/M ).t ▷ Φ';x :
A,Γ'' |
|
|
où Γ'=x : A,Γ''. Mais, puisque il est évident que
x∉ FV(ξ), nous savons par le
lemme 54 que
Φ';Γ''⊢ξ ↝ K et donc nous avons
une preuve se terminant comme suit:
|
| | Φ;Γ⊢ t ▷ Φ';Γ'
Φ';Γ'⊢ξ ↝ K |
|
| Φ;Γ⊢ ξ [ t ] ↝ K |
|
|
Ce qui est le résultat attendu.
- Si s=( ψP : A/K ).t où ψ≠ξ et si
ξ [ ( ψP : A/K ).t ] → ξ [ t ] ,
nous raisonnons comme dans le cas 1.
- Si s=( ξP :
A/K ).t et si ξ [ ( ξP :
A/K ).t ] → K nous concluons en appliquant la règle
(Left) ou la règle (Right).
- Si M=[Ξ ∣ s M1,M2 ] alors nous connaissons une
preuve pour
Φ ;Γ ⊢ [Ξ ∣ s M1,M2 ] : A. Par le
corollaire 45,
nous pouvons de plus supposer que Γ=Des(Γ). Nous avons
alors 3 possibilités:
-
Si Ξ =
L et si [L ∣ s M1,M2 ]→
M1 [ s ] , nous avons alors, par le
lemme 48, une preuve se
terminant par:
|
|
| Φ ;Γ ⊢L ↝ L |
| Φ ;Γ ⊢ M1 [ s ] : A |
| Φ ;Γ ⊢ M2 [ s ] : A |
|
|
| Φ ;Γ ⊢[L ∣ s M1,M2 ] : A |
|
|
Le résultat est alors évident.
- Si Ξ =
R et si [R ∣ s M1,M2 ]→
M2 [ s ] , nous raisonnons comme dans le cas
1.
- Si Ξ =
ξ et si [ξ ∣ s M1,M2 ]→
[ξ ∣ M1 [ s ] , M2 [ s ] ], alors, par le
lemme 48, nous avons une
preuve se terminant comme suit:
|
|
| Φ;Γ'⊢ξ ↝ ξ |
| Φ;P : B,Γ'⊢ M1 [ s ] : A |
| Φ;Q : C,Γ'⊢ M2 [ s ] : A |
| |
|
|
| Φ;[ξ ∣ P,Q ] :
B+C,Γ'⊢[ξ ∣ s M1,M2 ] : A |
|
|
où Γ=[ξ ∣ P,Q ] : A+B,Γ'. Nous tirons de cette preuve la
preuve suivante:
|
|
| Φ;Γ'⊢ξ ↝ ξ |
| Φ;P : B,Γ'⊢ M1 [ s ] : A |
| Φ;Q : C,Γ'⊢ M2 [ s ] : A |
| |
|
|
| Φ;[ξ ∣ P,Q ] :
B+C,Γ'⊢[ξ ∣ M1 [ s ] , M2 [ s ] ] : A |
|
|
- Si M= M1 [ s ] alors par le
corollaire 45, nous pouvons supposer
que Γ=Des(Γ). De même, par par le
lemme 50, nous avons une preuve se
terminant par:
|
| | Φ ;Γ ⊢
s ▷ Φ';ΓΓ' Φ';ΓΓ'⊢
M : A |
|
| Φ ;Γ ⊢ M1 [ s ] : A |
| (term)
|
Nous raisonnons maintenant différemment suivant la réduction
effectuée.
-
Si M1= M2 M3 et si
M1 [ s ] → M2 [ s ] M3 [ s ] nous
avons alors, par le
lemme 47, une preuve se
terminant par:
|
| | Φ';ΓΓ'⊢ M2 :
C→A Φ';ΓΓ'⊢ M3 : C |
|
| Φ';ΓΓ'⊢ M2 M3 : A |
|
|
Mais, puisque M1 ne peut pas contenir de variable de choix
libre (car la règle (term) est applicable), nous avons une
preuve se terminant par:
|
|
| Φ ;Γ ⊢ s ▷ Φ';ΓΓ' |
| Φ';ΓΓ'⊢ M2 : C→A |
|
|
| Φ ;Γ ⊢ M2 [ s ] : C→A |
| Φ ;Γ ⊢ s ▷ Φ';ΓΓ' |
| Φ';ΓΓ'⊢ M3 : C |
|
|
| Φ ;Γ ⊢ M3 [ s ] : C |
|
|
| Φ ;Γ ⊢ M2 [ s ] M3 [ s ] : A |
|
|
Ce qui est le résultat attendu.
- Si M1=inlC(M2), M1=inrC(M2) ou
M=⟨ M2, M3 ⟩, nous raisonnons comme dans le
cas 1.
- Si M1=[ξ ∣ M2,M3 ] et si
[ξ ∣ M2,M3 ] [ s ] → [ ξ [ s ] ∣ s M2,M3 ],
par le lemme 48 deux possibilités s'offrent à nous:
-
S'il existe une preuve de
Φ';ΓΓ'⊢[ξ ∣ M2,M3 ] : A se
terminant par une utilisation de la règle (Case1), cette
preuve se termine alors par:
|
|
| Φ';Γ'''⊢ξ ↝ ξ |
| Φ';P : B,Γ'''⊢ M2 : A |
| Φ';Q : C,Γ'''⊢ M3 : A |
|
|
| Φ';[ξ ∣ P,Q ] : B+C,Γ'''⊢
[ξ ∣ M2,M3 ] : A |
|
|
où [ξ ∣ P,Q ] : B+C,Γ'''=ΓΓ'. Par définition des
règles de dérivation de types, nous savons que FV(s) ne
contient pas de variable de choix. Nous en déduisons grâce au
lemme 55 que
FV(s)∩ BV([ξ ∣ P,Q ]). Ainsi par le
lemme 54, nous obtenons une preuve de
Φ;Γ'';⊢ s ▷ Φ';Γ''Γ' et, partant de là, grâce au
lemme 41, des preuves de Φ;P :
B,Γ'';⊢s ▷ Φ';P : B,Γ''Γ'
et de Q : C,Φ;Γ'';⊢ s ▷ Φ';Q : C,Γ''Γ'. Nous déduisons de
ces trois preuves les preuves suivantes:
|
| | Φ;Γ''⊢
s ▷ Φ';Γ''Γ'
Φ';Γ''Γ'⊢ξ ↝
ξ |
|
| Φ;Γ'';⊢ ξ [ s ] ↝ ξ |
|
|
|
| | Φ;P : B,Γ''⊢
s ▷ Φ';P : B,Γ''Γ'
Φ';P : B,Γ''Γ'⊢ M2 : A |
|
| Φ;Γ'';⊢ M2 [ s ] ↝ A |
|
|
et
|
| | Φ;Q : C,Γ''⊢
s ▷ Φ';Q : C,Γ''Γ'
Φ';Q : C,Γ''Γ'⊢ M3 : A |
|
| Φ;Γ'';⊢ M3 [ s ] : A |
|
|
Nous concluons alors grâce à la règle (Frozencase1).
- S'il existe une preuve de
Φ';ΓΓ'⊢[ξ ∣ M2,M3 ] : A se
terminant par une utilisation de la règle (Case2), cette
preuve se termine alors par:
|
| | Φ ';Γ '⊢ ξ ↝ K Φ ';Γ '⊢
M1 : A Φ ';Γ '⊢ M2 : A |
|
| Φ ';Γ '⊢
[ξ ∣ M1,M2 ] : A |
|
|
Nous en déduisons de manière évidente la preuve suivante:
|
|
| Φ ;Γ ⊢ s ▷ Φ ';Γ ' |
| Φ ';Γ '⊢ ξ ↝ K |
|
|
| Φ ;Γ ⊢ ξ [ s ] ↝ K |
| Φ ;Γ ⊢ s ▷ Φ ';Γ ' |
| Φ ';Γ '⊢ M1 : A |
|
|
| Φ ;Γ ⊢ M1 [ s ] ↝ A |
| Φ ;Γ ⊢ s ▷ Φ ';Γ ' |
| Φ ';Γ '⊢ M2 : A |
|
|
| Φ ;Γ ⊢ M2 [ s ] ↝ A |
|
|
| Φ ;Γ ⊢[ ξ [ s ] ∣ s M1,M2 ] :
A |
|
|
- S'il existe une preuve de
Φ';ΓΓ'⊢[ξ ∣ M2,M3 ] : A se
terminant par une utilisation de la règle (Left) ou de la
règle (Right), nous raisonnons comme dans le cas précédent.
- Si M1=x quatre possibilités s'offrent alors à nous:
-
Si s=id et si x [ id ] → x, le résultat est
immédiat.
- Si s=( x/N ).t et x [ ( x/N ).t ] → N
alors, par les lemmes 49
et 50, nous avons une preuve se
terminant comme suit:
|
|
| Φ ;Γ ⊢ N : A |
| Φ ;Γ ⊢ t ▷ Φ';Γ''Γ |
|
|
| Φ ;Γ ⊢( x/N ).t ▷ Φ';x :
A,Γ''Γ |
Φ';x :
A,Γ''Γ⊢ x : A |
|
| Φ ;Γ ⊢ x [ ( x/N ).t ] : A |
|
|
D'où le résultat.
- Si s=( y/N ).t avec x≠ y et si x [ ( y/N ).t ] → x [ t ]
alors par les lemmes 49
et 50 nous avons une preuve se
terminant comme suit:
|
|
| Φ ;Γ ⊢ N : A |
| Φ ;Γ ⊢ t ▷ Φ';Γ''Γ |
|
|
| Φ ;Γ ⊢( y/N ).t ▷ Φ';y :
A,Γ''Γ |
Φ';y :
A,Γ''Γ⊢ x : A |
|
| Φ ;Γ ⊢ x [ ( y/N ).t ] : A |
|
|
Mais par le lemme 54, nous avons une preuve
de Φ';Γ''Γ⊢ x : A d'où nous
tirons:
|
| | Φ ;Γ ⊢ t ▷
Φ';Γ''Γ Φ';Γ''Γ⊢
x :
A |
|
| Φ ;Γ ⊢ x [ t ] : A |
|
|
- Si s=( ξP : A/K ).t et si
x [ ( ξP : A/K ).t ] → x [ t ] , nous
raisonnons comme dans le cas précédent.
- Si M1= M2 [ t ] et si
M2 [ t ] [ s ] → M2 [ t ∘ s ] , nous
avons alors, par le lemme 50, une
preuve se terminant comme suit:
|
| Φ ;Γ ⊢ s ▷ Φ';Γ'Γ
| Φ';Γ'Γ⊢ t ▷
Φ '';Γ '' |
| Φ '';Γ ''⊢ M2 : A |
|
|
| Φ';Γ'Γ⊢ M2 [ t ] :
A |
|
|
| Φ ;Γ ⊢ M2 [ t ] [ s ] : A |
|
|
Nous en déduisons la preuve suivante:
|
|
| Φ ;Γ ⊢ s ▷ Φ';Γ'Γ |
| Φ';Γ'Γ⊢ t ▷ Φ '';Γ '' |
|
|
| Φ ;Γ ⊢t ∘ s ▷ Φ '';Γ '' |
Φ '';Γ ''⊢ M2 : A |
|
| Φ ;Γ ⊢ M2 [ t ∘ s ] : A |
|
|
- Si M= M1 M2 alors par le
lemme 47, nous avons une
preuve se terminant par:
|
| | Φ ;Γ ⊢ M1 : B→A Φ ;Γ ⊢ M2 :
B |
|
| Φ ;Γ ⊢ M1 M2 : A |
|
|
Nous raisonnons alors par cas sur la réduction:
-
Si M1=λ P. N et si
λ P : B. N M2→ (λ P : B. N) [ id ] M2, nous avons alors par le lemme 47, une preuve se terminant par:
|
|
| Φ ;Γ ⊢ id ▷ Φ ;Γ
Φ ;Γ ⊢λ P : B. N :
B→A |
|
| Φ ;Γ ⊢ (λ P : B. N) [ id ] :
B→A |
Φ ;Γ ⊢ M2 :
B |
|
| Φ ;Γ ⊢ (λ P : B. N) [ id ] M2 : A |
| |
|
|
- Si B=B1× B2, M1= (λ ⟨ P1, P2 ⟩ :
B1× B2. N) [ s ] , M2=⟨ N1, N2 ⟩ et si (λ ⟨ P1, P2 ⟩ :
B1×
B2. N) [ s ] ⟨ N1, N2 ⟩→ ( (λ P1 : B1. λ P2 : B2. N) [ s ] N1) N2, nous commençons par remarquer que par le corollaire 45, nous pouvons supposer que Γ=Des(Γ). De plus, par le lemme 50 nous connaissons une preuve se terminant par:
|
| | Φ ;Γ ⊢ s ▷ Φ ';Γ ' Φ ';Γ '⊢λ ⟨ P1, P2 ⟩ :
B1×
B2. N : (B1× B2) → A |
|
| Φ ;Γ ⊢ (λ ⟨ P1, P2 ⟩ :
B1×
B2. N) [ s ] : (B1× B2) → A |
|
|
De même, par le lemme 47 nous
connaissons deux preuves se terminant par:
|
| | Φ ;Γ ⊢ N1 : B1 Φ ;Γ ⊢ N2 : B2 |
|
| Φ ;Γ ⊢⟨ N1, N2 ⟩ : B1× B2 |
|
|
et
|
| | Φ';⟨ P1, P2 ⟩ : B1× B2,Γ'⊢
N : A |
|
| Φ ';Γ '⊢λ ⟨ P1, P2 ⟩ : B1×
B2. N : (B1× B2)→ A |
|
|
Donc par le corollaire 45, nous
avons la
preuve suivante:
|
| Φ ;Γ ⊢
s ▷ Φ ';Γ '
| Φ';P2 : B2,P1 :
B1,Γ'⊢ N : A |
|
| Φ';P1 :
B1,Γ'⊢λ P2. N : B2→A |
|
|
| Φ ';Γ '⊢λ P1 : B1. λ P2 :
B2. N : B1→B2→A |
|
|
| Φ ;Γ ⊢ (λ P1 : B1. λ P2 :
B2. N) [ s ] : B1→B2→A |
| |
|
|
D'où nous déduisons l'existence de la preuve suivante:
|
|
| Φ ;Γ ⊢ (λ P1 : B1. λ P2 :
B2. N) [ s ] : B1→B2→A |
| Φ ;Γ ⊢ N1 : A1 |
|
|
| Φ ;Γ ⊢ (λ P1 :
B1. λ P2 : B2. N) [ s ] N1 : B2→ A |
Φ ;Γ ⊢ N2 : A2 |
|
| Φ ;Γ ⊢ ( (λ P1 :
B1. λ P2 : B2. N) [ s ] N1) N2 : A |
| |
|
|
- Si M1= (λ @(P1,P2) :
B. N) [ s ] et si (λ @(P1,P2) :
B. N) [ s ] M2→ ( (λ P1 :
B. λ P2 : B. N) [ s ] M2) M2, nous
raisonnons comme dans le cas précédent.
- Si B=B1+ B2, M1= (λ [ξ ∣ P1,P2 ] :
B1+ B2. N) [ s ] , M2=inlB2(N1) et si
| (λ | ⎡
⎣ | ξ ∣ P1,P2 | ⎤
⎦ | :
B1+
B2. N) [ s ] inlB2(N1)→ |
|
| (λ P1 :
B1. N) [ ( ξP2 : B2/L ).s ] N1 |
|
Par le lemme 50, nous
connaissons une preuve se terminant comme suit:
|
| | Φ ;Γ ⊢ s ▷ Φ ';Γ ' Φ ';Γ '⊢λ [ξ ∣ P1,P2 ] :
B1+
B2. N : (B1+B2)→A |
|
| Φ ;Γ ⊢ (λ [ξ ∣ P1,P2 ] :
B1+
B2. N) [ s ] : (B1+B2)→A |
| |
|
|
Mais alors, par le
lemme 48, nous avons la
preuve suivante:
|
| | Φ';[ξ ∣ P1,P2 ] : B1+B2,Γ'⊢ N :
A |
|
| Φ ';Γ '⊢λ [ξ ∣ P1,P2 ] :
B1+B2. N : (B1+B2)→A |
|
|
d'où nous déduisons, par le
lemme 52, une preuve de
ξ : L,Φ';P1 : B1,P2 :
B2,Γ'⊢ N : A
De plus, par le lemme 47, nous
connaissons une preuve se terminant comme suit:
|
| | Φ ;Γ ⊢ N1 : A1 |
|
| Φ ;Γ ⊢inlB2(N1) : B1+B2 |
|
|
Nous déduisons de ce qui précède les deux preuves suivantes:
|
| | Φ ;Γ ⊢ s ▷ Φ ';Γ ' |
|
| Φ ;Γ ⊢
( ξP2 : B2/L ).s
▷ ξ : L,Φ;P2 :
B2,Γ' |
|
|
et
|
| | ξ : L,Φ;P1 : B1,P2 :
B2,Γ'⊢ N : A |
|
| ξ : L,Φ;P2 :
B2,Γ'⊢λ P1 :
B1. N : B1→A |
|
|
Ce qui nous fournit une preuve de
| Φ ;Γ ⊢ (λ P1 :
B1. N) [ ( ξP2 : B2/L ).s ] : B1→A
|
Nous concluons alors en combinant cette dernière preuve avec la
preuve, par nous connue, de Φ ;Γ ⊢ N1 : A.
- Si B=B1+ B2, M1= (λ [ξ ∣ P1,P2 ] :
B1+ B2. N) [ s ] , M2=inrB1(N1) et si
| | | (λ | ⎡
⎣ | ξ ∣ P1,P2 | ⎤
⎦ | :
B1+
B2. N) [ s ] inrB1(N1)→ |
|
| (λ P2 :
B2. N) [ ( ξP1 : B1/R ).s ] N1 |
|
nous raisonnons comme dans le cas précèdent.
- Si M1= (λ x : B. N) [ s ] et si
(λ x :
B. N) [ s ] M2→ N [ ( x/M2 ).s ] , alors
par le corollaire 45, nous pouvons
supposer que Γ=Des(Γ). Par le lemme 50, nous connaissons
la preuve suivante:
|
| | Φ ;Γ ⊢ s ▷ Φ ';Γ ' λ x :
B. N : B→ A |
|
| Φ ;Γ ⊢ (λ x :
B. N) [ s ] : B→A |
|
|
Par le lemme 47, nous
connaissons
la preuve suivante:
|
| | Φ';x : A,Γ'⊢ N : B |
|
| Φ ';Γ '⊢λ x :
B. N : B→A |
|
|
Nous en déduisons:
|
|
| Φ ;Γ ⊢ M2 ▷ A Φ ;Γ ⊢ s ▷ Φ ';Γ ' |
|
| Φ ;Γ ⊢
( x/M2 ).s ▷ Φ';x :
A,Γ' |
Φ';x : A,Γ'⊢ N : A |
|
| Φ ;Γ ⊢ N [ ( x/M2 ).s ] : A |
|
|
- Si M1= (λ _ : B. N) [ s ] et si
(λ _ :
B. N) [ s ] M2→ N [ s ] , nous raisonnons comme
dans le cas précédent.
Nous avons donc démontré la propriété de préservation de types par
réduction. Nous allons maintenant nous servir de cette propriété pour
démontrer la propriété de normalisation forte pour les expressions
bien typées.
4.4 Normalisation forte pour λ Pw
4.4.1 Préliminaires
Cette section est consacrée à la démonstration de la normalisation
forte des expressions bien typées du calcul λ Pw. Nous allons pour
cela utiliser une technique de preuve due à Ritter [Rit94].
Cette technique est fondée sur celle bien connue de la réductibilité.
L'originalité de la preuve de Ritter est de remplacer l'étude de la
normalisation forte du calcul par l'étude de celle d'un second calcul
dont les expressions sont celles du premier modulo une théorie
équationnelle. Notre démarche peut se résumer comme suit:
-
Nous commencerons par définir un nouveau formalisme appelé
λ Pw/≡-calcul.
- Nous définirons alors la notion d'expression réductible
dans le λ Pw/≡-calcul.
- Nous montrerons que toute expression réductible du
λ Pw/≡-calcul est fortement normalisable.
- Nous montrerons que si la substitution s est réductible alors
pour tout terme bien typé M (resp. toute substitution bien typée
t) le terme M [ s ] (resp. la substitution
t ∘ s) est réductible.
- Il ne nous restera plus alors qu'à remarquer que la
substitution id est réductible pour conclure à la normalisation
forte du λ Pw/≡-calcul. En effet, si, par exemple, M est un terme
bien typé, M [ id ] sera réductible donc fortement
normalisable et donc M sera lui-même fortement normalisable.
- Enfin, le lemme 8 nous donnera la
normalisation forte du λ Pw-calcul.
Mais avant toute chose nous allons définir les substitutions de
choix qui sont les substitutions qui ne lient pas de variables
usuelles.
Définition 57 (Substitution de choix)
L'ensemble SC des substitutions de
choix est défini comme étant le plus petit ensemble de
substitutions stable par concaténation et tel que:
-
id∈ SC
- ( ξP : A/K ).s∈ SC si s∈ SC et
BV(P)=∅.
Les substitutions de choix sont, en fait, une généralisation des
substitutions inopérantes (définition 12) au
cas du λ Pw-calcul.
Il est évident que:
Remarque 58
-
Si s∈ SC et si s→ s' alors s'∈ SC.
- Si s∈ SC alors s est fortement normalisable.
Nous avons de plus:
Lemme 59
Soit s une substitution telle que Ψ;Δ⊢
s ▷ Φ;∅ alors:
-
Δ=∅.
- s est une substitution de choix.
-
- Preuve.
Le premier point est évident grâce à la
remarque 40. Pour le second point,
nous raisonnons par contradiction. Supposons que s ne soit pas
une substitution de choix. Alors il est évident que
Δ≠∅.
Nous allons maintenant donner la définition du calcul λ Pw/≡.
4.4.2 Définition de λ Pw/≡
Nous définissons la relation de congruence ≡ sur les
expressions du calcul λ Pw comme étant la plus petite congruence
telle que:
| | | ( M N) [ s ] | ≡ | M [ s ] N [ s ] |
| M [ s ] [ t ] | ≡ | M [ s ∘ t ] |
| (s ∘ t) ∘ u | ≡ | s ∘ (t ∘ u) |
|
Nous définissons alors l'ensemble des expressions du λ Pw/≡-calcul
comme étant l'ensemble des classes d'équivalences de la relation
≡. Nous définissons alors la relation de réduction →λ Pw/≡ sur
les expressions du λ Pw/≡-calcul comme suit:
Soit e1 et e2 deux expressions du λ Pw/≡-calcul, nous avons
e1→λ Pw/≡ e2 si et seulement si il existe deux λ Pw-expressions
e1' et e2' telles que: e1≡ e1'→λ Pw e2'≡
e2
Nous remarquons que la définition de la relation ≡ étant
fondée sur des règles de réduction de →λ Pw , le calcul λ Pw/≡
possède lui aussi la propriété de préservation de types par
réduction.
Nous allons maintenant définir la notion d'expression
réductible et étudier cette notion.
4.4.3 Expression du λ Pw/≡-calcul réductible
Nous allons dans un premier temps définir la notion, vitale pour la
suite, de terme et de substitution neutre. Informellement, les
termes et substitutions neutres sont les termes et les substitutions
qui, une fois appliqués ou concaténés à une expression ne créent pas
de radical.
Définition 60 (Termes et substitutions
neutres)
-
Un terme est dit neutre si et seulement si il n'est pas de la
forme (λ P. M) [ s ] , inlA(M), inrB(M) ou
⟨ M1, M2 ⟩.
- Une substitution est dite neutre si et seulement si elle n'est pas de la
forme ( x/M ).t.
Notation 61
Dans toute la suite de cette section nous utiliserons les notations
suivantes:
-
PA× B1(M) =def
(λ ⟨ x, _ ⟩ : A× B. x) [ id ] M où
x est une variable fraîche.
- PA× B2(M) =def
(λ ⟨ _ , x ⟩ : A× B. x) [ id ] M où
x est une variable fraîche.
- SA+B(M)=def (λ [ξ ∣ x,y ] : A+
B. [ξ ∣ ⟨ x, w2 ⟩,⟨ w2, y ⟩ ]) [ id ] M où
x, y, w1, w2 et ξ sont des variables fraîches.
Enfin, comme au chapitre 3, nous utiliserons la
notation ν(e) pour dénoter la longueur de la plus longue
séquence de réductions issue de e.
Nous définissons maintenant les ensembles d'expressions réductibles.
Informellement, nous voulons avoir:
-
Les termes réductibles de type ι sont les termes de type
ι qui sont fortement normalisables.
- Les termes réductibles de type A→ B sont les termes de type
A→ B tels que M N soit réductible de type B pour
tout N réductible de type A.
- ⟨ M1, M2 ⟩ est réductible de type A× B est réductible
si et seulement si M1 et M2 sont réductibles de type A et
B.
- inlB(M) et inrA(M) est réductible si et seulement si
M est réductible.
- Les substitutions réductibles sont les substitutions bien
typées qui ne contiennent que des termes réductibles.
Définition 62 (Termes et substitutions réductibles)
-
L'ensemble des termes réductibles pour un environnement
Φ;Γ et un type A est défini par induction
sur A comme suit:
-
- [[ ι]]Φ ;Γ =def {M∣ Φ ;Γ ⊢
M : ι et M est fortement
normalisable}
- [[ A→ B]]Φ ;Γ =def {M ∣ Φ ;Γ ⊢ M :
A et ∀
N∈[[ A]]Φ;ΓΔ,
( M N)∈[[ B]]Φ;ΓΔ }
où BV(Δ)∩ ( BV(Φ;Γ)∪ FV(M))
et Δ est linéaire et compatible.
- [[ A× B]]Φ ;Γ =def {M ∣ Φ ;Γ ⊢ M :
A× B, PA× B1(M)∈[[ A]]Φ ;Γ et
PA× B2(M)∈[[ B]]Φ ;Γ }
- [[ A+B]]Φ ;Γ M=def{ M∣ Φ ;Γ ⊢ M : A+B
et SA+B(M)∈[[ A× B]]Φ;w1 :
A,w2 : B,Γ}
- L'ensemble des substitutions réductibles pour un environnement
Φ ;Γ dans un environnement Ψ;Δ est
défini comme suit:
| [[ Φ ;Γ ]]Ψ;Δ=def{s∣
Ψ;Δ⊢ s ▷ Φ ;Γ et ∀
(x : A)∈Γ, x [ s ] ∈[[ A]]Φ ;Γ }
|
Dans la suite de cette section, il nous arrivera parfois d'écrire
qu'un terme (ou une substitution) est réductible sans préciser de
type ni d'environnement de types quand ceux-ci sont évidents par le
contexte ou quand ils ne sont pas nécessaires à la démonstration.
Les termes réductibles satisfont les propriétés suivantes:
Lemme 63
Soit A un type, nous avons:
-
Si M∈[[ A]]Φ ;Γ
alors M est fortement normalisable.
- Si
Φ ;Γ ⊢( x M1 … Mn) : A
et si les termes M1,…,Mn sont fortement normalisables alors
( x M1 … Mn)∈[[ A]]Φ ;Γ .
- Si
M∈[[ A]]Φ ;Γ et si M→ M' alors M'∈[[ A]]Φ ;Γ .
- Si M est un terme
neutre tel que Φ ;Γ ⊢ M : A et tel que tous ses
réduits en un pas sont dans [[ A]]Φ ;Γ , alors
M∈[[ A]]Φ ;Γ .
-
- Preuve.
Nous raisonnons par induction sur le type A.
-
Si A=ι, nous raisonnons comme suit:
-
Par définition de [[ ι]]Φ ;Γ .
- Par la forme du terme
M=( x M1 … Mn), nous savons que
toute réduction de M doit obligatoirement avoir lieu à
l'intérieur des Mi et que le résultat obtenu est encore de
cette forme. Donc toute séquence de réduction de M est
obligatoirement finie. En conséquence, par définition de
[[ ι]]Φ ;Γ ,
( x M1 … Mn)∈[[ ι]]Φ ;Γ .
- Soit un terme M∈[[ ι]]Φ ;Γ . Par définition de
[[ ι]]Φ ;Γ , on a Φ ;Γ ⊢ M : ι, et M
est fortement normalisable. Donc, tout terme M' tel que
M→ M', est aussi fortement normalisable. De plus, par le
théorème 56, nous savons que
Φ ;Γ ⊢ M' : ι et donc, par définition de
[[ ι]]Φ ;Γ , M'∈[[ ι]]Φ ;Γ .
- Soit M un terme neutre tel que Φ ;Γ ⊢ M : ι
et tel que tous ses réduits en un pas appartiennent à
[[ ι]]Φ ;Γ . Alors, par définition de
[[ ι]]Φ ;Γ , tous les réduits en un pas de M sont
fortement normalisables et donc M est lui même fortement
normalisable. En conséquence, par définition de
[[ ι]]Φ ;Γ , donc M∈[[ ι]]Φ ;Γ .
- Si A=A1→A2 nous raisonnons comme suit:
-
Soit M un terme appartenant à l'ensemble
[[ A1→A2]]Φ ;Γ . Par hypothèse d'induction
(point 2 avec n=0), si
x∉Γ, le terme x appartient a l'ensemble
[[ A1]]Φ;x : A1,Γ. Par
définition de [[ A1→ A2]]Φ ;Γ ,
M x∈[[ A2]]Φ;x : A1,Γ,
et donc par hypothèse d'induction (point 1),
M x est fortement normalisable. Nous en déduisons que
M est lui même fortement normalisable.
- Soit un terme
M=( x M1 … Mn) tel que
Φ ;Γ ⊢ M : A1→ A2 et tel que tous les Mi
soient fortement normalisables. Soit
N∈[[ A1]]Φ;ΔΓ. Par hypothèse d'induction
(point 1), N est fortement
normalisable. De plus, par le lemme 41, nous
savons que Φ;ΔΓ⊢ M : A1→A2.
Nous en déduisons que Φ;ΔΓ⊢
( x M1 … Mn N) : A2.
Nous savons alors, par hypothèse d'induction
(point 2) que le terme
( x M1 … Mn N)
appartient à l'ensemble
[[ A2]]Φ;ΔΓ. Puisque nous
n'avons fait aucune hypothèse particulière ni sur Δ ni
sur N au cours de cette démonstration, nous pouvons en
déduire que le terme
( x M1 … Mn) appartient à
l'ensemble [[ A1→ A2]]Φ ;Γ .
- Soit un terme M de l'ensemble [[ A1→ A2]]Φ ;Γ .
Considérons un terme M' tel que M→ M'. Le
théorème 56, nous assure que
Φ ;Γ ⊢ M' : A1→A2. Soit maintenant un terme N
de l'ensemble [[ A1]]Φ;ΔΓ.
Par définition de [[ A1→ A2]]Φ ;Γ , nous savons que
( M N)∈[[ A2]]Φ;ΔΓ.
Par hypothèse d'induction (point 3), nous
en déduisons que
( M' N)∈[[ A2]]Φ;ΔΓ.
Ce qui nous permet de conclure que M'∈[[ A1→A2]]Φ ;Γ .
- Soit M un terme neutre tel que Φ ;Γ ⊢ M :
A1→A2 et tel que tous ses réduits en un pas soient dans
[[ A1→A2]]Φ ;Γ . Soit N un terme appartenant à
l'ensemble [[ A1]]Φ;ΔΓ. Nous
devons montrer que
( M N)∈[[ A2]]Φ;ΔΓ.
Par le lemme 41,l nous savons que
Φ;ΔΓ⊢ ( M N) : B. Nous
remarquons de plus que le terme ( M N) est neutre.
Donc, si nous arrivons à montrer que tous les réduits de
( M N) sont réductibles, nous obtiendrons par hypothèse d'induction
(point 4) que ce terme
est dans l'ensemble
[[ A2]]Φ;ΔΓ. Nous remarquons
de plus que par hypothèse d'induction
(point 1), M et N sont
fortement normalisables. Nous raisonnons donc, pour montrer que
tous les réduits de M N sont dans
[[ A2]]Φ;ΔΓ, par récurrence
sur ν(M)+ν(N) puis par cas sur les différents
réduits possibles.
-
Si M N M N' où N→ N' alors il
est évident que ν(N')<ν(N) et nous obtenons le
résultat par hypothèse d'induction.
- Si M N M' N où M→ M' alors il
est évident que ν(M')<ν(M) et nous obtenons le
résultat par hypothèse d'induction.
- Aucun autre cas n'est possible puisque M est un terme
neutre (définition 60).
- Si A=A1× A2, nous raisonnons comme suit:
-
Soit M un terme de l'ensemble [[ A1× A2]]Φ ;Γ ,
par définition de [[ A1× A2]]Φ ;Γ nous savons que
PA1× A21(M)∈[[ A1]]Φ ;Γ . Par hypothèse d'induction
(point 1), nous en déduisons
que PA1× A21(M) est fortement normalisable.
D'où nous déduisons trivialement que M est fortement
normalisable.
- Soit M=( x M1 … Mn) tel que
Φ ;Γ ⊢ M : A1× A2 et tel que tous les Mi
soient fortement normalisables. Nous devons montrer que
PA1× A21(M) et PA1× A22(M) sont
respectivement dans [[ A1]]Φ ;Γ et [[ A2]]Φ ;Γ .
Nous ne montrons ici que l'appartenance de PA1×
A21(M) à l'ensemble [[ A1]]Φ ;Γ , le second cas étant
similaire. Nous raisonnons, pour cela, par récurrence sur
σ=∑i ν(Mi).
-
Si σ=0 alors PA1× A21(M) est un
terme neutre qui ne possède pas de réduits et tel que
Φ ;Γ ⊢ PA1× A21(M) : A1. Donc par
hypothèse d'induction (point 4), le
terme PA1× A21(M) appartient à
[[ A1]]Φ ;Γ .
- Si σ>0 alors les seuls réduits possibles en un pas de
PA1× A21(M) sont de la forme PA1×
A21(M') où
M=( x M1 … Mi' … Mn)
avec Mi→ Mi'. Or, par hypothèse d'induction sur σ,
PA1× A21(M') est bien dans [[ A1]]Φ ;Γ
et donc PA1× A21(M) est bien dans
[[ A1]]Φ ;Γ
- Soit M∈[[ A1× A2]]Φ ;Γ et soit M' un terme tel
que M→ M'. Nous devons montrer que PA1×
A21(M') et PA1× A22(M') sont respectivement
dans [[ A1]]Φ ;Γ et [[ A2]]Φ ;Γ . Nous ne montrons
ici que la première appartenance, l'autre cas étant similaire.
Par la définition 62, nous savons que
PA1× A21(M)∈[[ A1]]Φ ;Γ . Nous remarquons
alors que PA1× A21(M) PA1×
A21(M'). Et donc, par hypothèse d'induction
(point 3),
PM'1(∈)[[ A1]]Φ ;Γ .
- Soit M un terme neutre tel que Φ ;Γ ⊢ M : A1×
A2 et tel que tous ses réduits en un pas soient dans
[[ A1× A2]]Φ ;Γ . Nous devons montrer que
PA1× A21(M) et PA1× A22(M) sont
respectivement dans [[ A1]]Φ ;Γ et [[ A2]]Φ ;Γ .
Nous ne montrons ici que la première appartenance l'autre cas
étant similaire. M étant neutre
(définition 60), nous savons que les
réduits en un pas de PA1× A21(M) sont de la
forme PA1× A21(M') où M→ M'. Mais, par
hypothèse, nous savons que M'∈[[ A1× A2]]Φ ;Γ , d'où
nous déduisons par la définition 62 que
PA1× A21(M') est dans [[ A1]]Φ ;Γ . Nous
concluons alors grâce à l'hypothèse d'induction
(point 4) sur A1.
- Si A=A1+ A2, nous raisonnons comme suit:
-
Soit M un terme de l'ensemble [[ A1+ A2]]Φ ;Γ . Par
définition de [[ A1+ A2]]Φ ;Γ , nous savons que
SA1+ A2(M)∈[[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ. Or nous venons de montrer
que tout élément de [[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ est fortement normalisable.
Donc SA1+A2(M) est fortement normalisable. Nous
en déduisons que M est lui-même fortement normalisable.
- Soit M=( x M1 … Mn) tel que
Φ ;Γ ⊢ M : A1+ A2 et tel que tous les Mi soient
fortement normalisables. Nous devons montrer que
SA1+ A2(M) est dans
[[ A1×
A2]]Φ;w1 : A1,w2 : A2,Γ . Nous raisonnons, pour cela, par récurrence sur
σ=∑i ν(Mi).
-
Si σ=0 alors SA1+ A2(M) est un terme
neutre qui ne possède pas de réduits et tel que
Φ;w1 : A1,w2 :
A2,Γ⊢ SA1+ A2(M) : A1× A2. Donc
par hypothèse d'induction (point 4) pour
A1× A2, le terme SA1+ A2(M) appartient à
[[ A1×
A2]]Φ;w1 : A1,w2 : A2,Γ.
- Si σ>0 alors les seuls réduits possibles en un pas de
SA1+ A2(M) sont de la forme SA1+
A2(M') où
M=( x M1 … Mi' … Mn)
avec Mi→ Mi'. Or, par hypothèse d'induction sur σ,
SA1+A2(M') est bien dans
[[ A1×
A2]]Φ;w1 : A1,w2 : A2,Γ et donc SA1+A2(M) est bien dans
[[ A1×
A2]]Φ;w1 : A1,w2 : A2,Γ
- Soit M∈[[ A1+ A2]]Φ ;Γ et soit M' un terme tel
que M→ M'. Nous devons montrer que SA1+
A2(M') est dans [[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ par la
définition 62. Or nous savons que
SA1+A2(M)∈[[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ. Mais, nous pouvons
remarquer que SA1+A2(M) SA1+A2(M').
Et donc, puisque la propriété est vrai pour A1× A2, nous
pouvons conclure
SA1+A2(M')∈[[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ.
- Soit M un terme neutre tel que Φ ;Γ ⊢ M : A1+
A2 et tel que tous ses réduits en un pas soient dans
[[ A1+ A2]]Φ ;Γ . Nous devons montrer que SA1+
A2(M) est dans [[ A1× A2]]Φ;w1 :
A1,w2 : A2,Γ. M étant neutre
(définition 60), nous savons que les
réduits en un pas de SA1+ A2(M) sont de la forme
SA1+ A2(M') où M→ M'. Mais, par hypothèse
M'∈[[ A1+ A2]]Φ ;Γ , d'où nous déduisons par la
définition 62 que SA1+ A2(M')
est dans [[ A1× A2]]Φ;w1 : A1,w2 :
A2,Γ. Nous concluons alors grâce au
point 4 sur A1× A2.
Nous avons aussi la propriété suivante:
Lemme 64
Soit M un terme appartenant à [[ A]]Φ ;Γ alors pour tout
environnement de types Ψ;Δ tel que
BV(Ψ;Δ)∩
( BV(Φ ;Γ )∪ FV(M))=∅,
M∈[[ A]]ΨΦ;ΔΓ
-
- Preuve.
Nous raisonnons par induction sur le type A.
-
Si A=ι, le résultat est immédiat par le
lemme 41.
- Si A=A1→A2, par le lemme 41, nous
savons que ΨΦ;ΔΓ⊢ M : A. Il ne
nous reste donc plus qu'a montrer que ∀
N∈[[ A1]]ΨΦ;Δ'ΔΓ, le
terme ( M N) est dans
[[ A2]]ΨΦ;Δ'ΔΓ. Cette
dernière appartenance est triviale par le
lemme 41 et la
définition 62.
- Si A=A1× A2, le résultat est immédiat par le
lemme 41 et par hypothèse d'induction.
- Si A=A1+ A2, le résultat est immédiat par le
lemme 41 et par hypothèse d'induction.
Nous remarquons aussi que nous avons:
Corollaire 65
Les variables sont réductibles.
-
- Preuve.
C'est le point 2 du
lemme 63.
Nous allons maintenant montrer des propriétés analogues pour les
substitutions.
Lemme 66
Les propriétés suivantes sont vraies:
-
Si la substitution s
appartient à l'ensemble
[[ Φ ;Γ ]]Ψ;Δ, alors s est
fortement normalisable.
- Si la substitution s
appartient à l'ensemble
[[ Φ ;Γ ]]Ψ;Δ, et si s→ s',
alors s' appartient aussi à cet ensemble.
- Si s est une
substitution neutre telle que Ψ;Δ⊢
s ▷ Φ ;Γ et telle que tous ses réduits en un pas
appartiennent à l'ensemble
[[ Φ ;Γ ]]Ψ;Δ, alors s
appartient aussi à cet ensemble.
-
- Preuve.
Nous raisonnons par cas sur Γ.
-
Si Γ=∅ nous raisonnons comme suit:
-
Soit s une substitution appartenant à l'ensemble
[[ Φ;∅]]Ψ;Δ.
Par le lemme 59, nous savons alors
que s est une substitution de choix. Nous obtenons alors le
résultat par la
remarque 58.
- Soit s une substitution appartenant à
[[ Φ;∅]]Ψ;Δ.
Par la définition 62, nous savons en
particulier que Ψ;Δ⊢ s ▷
Φ;∅. Soit alors s' une substitution telle
que s → s'. Par le
théorème 56, nous savons que
Ψ;Δ⊢ s' ▷ Φ;∅ et
donc s' est réductible par définition.
- Toute substitution s telle que
Ψ;Δ⊢ s ▷ Φ;∅ est
réductible par définition, et donc a fortiori les substitutions
neutres dont tous les réduits en un pas sont aussi réductibles.
- Si Γ≠∅ nous raisonnons comme suit:
-
Soit s une substitution appartenant à l'ensemble
[[ Φ ;Γ ]]Ψ;Δ. Nous
choisissons un couple (x : A)∈Γ. Par définition de
substitutions réductibles
x [ s ] ∈[[ A]]Ψ;Δ. Nous
en déduisons par le point 1 du
lemme 63, que x [ s ] est
fortement normalisable et donc que s en particulier est
fortement normalisable.
- Soit s une substitution appartenant à l'ensemble
[[ Φ ;Γ ]]Ψ;Δ. Nous avons
alors en particulier Ψ;Δ⊢ s ▷
Φ ;Γ . Soit maintenant s' une substitution telle que
s→ s'. Par le théorème 56,
nous savons que Ψ;Δ⊢ s' ▷ Φ ;Γ .
Pour montrer que s' est réductible, nous devons donc montrer
que ∀ (x : A)∈Γ,
x [ s' ] ∈[[ A]]Ψ;Δ.
Choisissons (x : A)∈Γ. Nous remarquons que
x [ s ] x [ s' ] . De plus, par définition des
substitutions réductibles, nous savons que x [ s ]
appartient à [[ A]]Ψ;Δ. Nous en
déduisons par le point 3
du lemme 63 que
x [ s' ] ∈[[ A]]Ψ;Δ.
- Soit s une substitution neutre telle que
Ψ;Δ⊢ s ▷ Φ ;Γ et telle que tous
ses réduits en un pas soient dans l'ensemble
[[ Φ ;Γ ]]Ψ;Δ. Nous devons
montrer que ∀ (x : A)∈Γ,
x [ s ] ∈[[ A]]Ψ;Δ. Soit
(x : A)∈Γ. Nous déduisons du fait que s est une
substitution neutre (définition 60), que
les seuls réduits en un pas de x [ s ] sont de la forme
x [ s' ] où s→ s'. Par le
théorème 56, nous savons que
Ψ;Δ⊢ s' ▷ Φ ;Γ et que s' est
réductible par hypothèse. Nous en déduisons que
x [ s' ] ∈[[ A]]Ψ;Δ par
définition des substitutions réductibles.
Nous avons aussi la propriété suivante:
Lemme 67
Soit s une substitution appartenant à
[[ Φ ;Γ ]]Ψ;Δ alors pour tout
environnement de types Ψ';Δ' tel que
BV(Ψ';Δ')∩
( BV(Φ ;Γ )∪ FV(s))=∅, on a:
-
- Preuve.
La preuve de ce lemme est immédiate par les
lemmes 41 et 63.
Nous remarquons aussi que:
Corollaire 68
Pour tout environnement de types compatible et linéaire Φ ;Γ ,
on a: id∈[[ Φ ;Γ ]]Φ ;Γ
Lemme 69
Soit s une substitution fortement normalisable alors pour toute
variable de choix ξ, le terme de choix ξ [ s ]
est fortement normalisable.
-
- Preuve.
Il nous suffit de montrer que tous les réduits en un par de
ξ [ s ] sont fortement normalisable. La preuve est
alors évidente par récurrence ν(s).
Nous allons maintenant donner des critères permettant de déterminer
si une expression est ou non réductible.
Lemme 70
Soient M un terme appartenant à [[ A]]Φ ;Γ et s une
substitution appartenant à [[ Ψ;Δ]]Φ ;Γ . Si
x est une variable usuelle fraîche, alors
t=( x/M ).s∈[[ Ψ;x : A,Δ]]Φ;x :
A,Γ.
-
- Preuve.
Nous commençons par remarquer que nous avons bien
Φ;x : A,Γ⊢ t ▷ Ψ;x :
A,Γ. Il nous suffit alors pour conclure de prouver que
∀ (y : B)∈ (x : A,Γ),
y [ t ] ∈[[ B]]Φ;x : A,Γ. Soit
(y : B)∈ (x : A,Γ). Puisque y [ t ] est un terme
neutre et bien typé, il nous suffit, par le
point 4 du
lemme 63, de montrer que tous ses
réduits en un pas sont dans [[ Ψ;x : A,Δ]]Φ;x :
A,Γ. Nous savons que M et
s sont respectivement dans [[ A]]Φ ;Γ et dans
[[ Ψ;x : A,Δ]]Φ ;Γ . Donc par le
point 1 du
lemme 63 et par le
point 1 du
lemme 66, nous savons que ces deux
expressions sont fortement normalisables. Nous allons donc montrer
que tous les réduits en un pas de t sont dans
[[ Ψ;x :
A,Δ]]Φ;x : A,Γ par récurrence sur ν(s)+ν(t), puis
par cas sur les réduits possibles..
-
Si y [ ( x/M ).s ] y [ ( x/M' ).s ]
où M→ M', nous concluons par hypothèse d'induction.
- Si y [ ( x/M ).s ] y [ ( x/M ).s' ]
où s→ s', nous concluons par hypothèse d'induction.
- Si y=x et si x [ ( x/M ).s ] → M, nous
concluons par hypothèse.
- Si y≠ x et si y [ ( x/M ).s ] y [ s ] , nous concluons par hypothèse.
Lemme 71
Soient s et t deux substitutions telles que
s ∘ t∈[[ Ψ;Δ]]Φ ;Γ et soit M un
terme tel que M [ t ] ∈[[ A]]Φ ;Γ , alors si x est une
variable fraîche, u=(( x/M ).s) ∘ t est dans
[[ Ψ;x : A,Δ]]Φ ;Γ .
-
- Preuve.
Nous devons tout d'abord démontrer que Φ ;Γ ⊢ u ▷
[[ Ψ;x : A,Δ]]Φ ;Γ . Or, nous savons que:
Φ ;Γ ⊢ s ∘ t ▷ Ψ;Δ. Par le
lemme 49 nous déduisons de ce fait la preuve
suivante:
|
| | Φ ;Γ ⊢ t ▷ Φ ';Γ ' Φ ';Γ '⊢
s ▷ Ψ;Δ |
|
| Φ ;Γ ⊢ s ∘ t ▷
Ψ;Δ |
|
|
De même, nous savons par hypothèse que
Φ ;Γ ⊢ M [ t ] : A et donc, grâce au
lemme 50, nous déduisons:
|
| | Φ ;Γ ⊢ t ▷ Φ ';Γ ' Φ ';Γ '⊢ M :
A |
|
| Φ ;Γ ⊢ M [ t ] : A |
|
|
Ces deux preuves nous permettent de construire la preuve suivante:
|
| Φ ;Γ ⊢ t ▷ Φ ';Γ '
| Φ ';Γ '⊢ M : A |
| Φ ';Γ '⊢ s : Ψ;Δ |
|
|
| Φ ';Γ '⊢( x/M ).s ▷ Ψ;x :
A,Δ |
|
|
| Φ ;Γ ⊢(( x/M ).s) ∘ t ▷ Ψ;x :
A,Δ |
|
|
Nous savons donc que
Φ ;Γ ⊢(( x/M ).s) ∘ t ▷ Ψ;x :
A,Δ. Il nous faut maintenant prouver que (y : B)∈
(x : A,Γ), y [ u ] ∈[[ B]]Φ ;Γ . Soit un tel (y :
B). Nous remarquons de plus que le terme y [ u ] est un
terme neutre. Par le point 4
du lemme 63, il nous suffit donc de
montrer que tous ses réduits en un pas appartiennent à
[[ B]]Φ ;Γ . Puisque les expressions M [ t ] et
s ∘ t sont réductibles, elles sont aussi fortement
normalisables par les point 1 des
lemmes 63
et 66. Nous raisonnons dès lors par
récurrence sur la somme
Σ=ν( M [ t ] )+ν(s ∘ t) puis par
cas sur les réduits en un pas de y [ u ] .
-
Si y [ (( x/M ).s) ∘ t ] y [ (( x/M' ).s) ∘ t ] avec M→ M', nous
obtenons le résultat par hypothèse d'induction.
- Si y [ (( x/M ).s) ∘ t ] y [ (( x/M ).s') ∘ t ] avec s→ s', nous
obtenons le résultat par hypothèse d'induction.
- Si y [ (( x/M ).s) ∘ t ] y [ (( x/M ).s) ∘ t' ] avec t→ t', nous
obtenons le résultat par hypothèse d'induction.
- Si y [ (( x/M ).s) ∘ t ] y [ ( x/ M [ t ] ).(s ∘ t) ] , nous
remarquons alors que puisque par hypothèse M [ t ] et
s ∘ t sont respectivement dans [[ A]]Φ ;Γ et
[[ Ψ;Δ]]Φ ;Γ , nous pouvons leur appliquer
le lemme 70 et ainsi
obtenir l'appartenance de
( x/ M [ t ] ).(s ∘ t) à [[ B]]Φ ;Γ . Ceci
nous permet de conclure.
Lemme 72
Soit s une substitution appartenant à
[[ Ψ;Δ]]Φ ;Γ . Soient aussi, ξ une
variable de choix fraîche, K une constante de choix, A un
type et P un motif linéaire tel que les variables apparaissant
dans P soient toutes fraîches. Soit alors la substitution
t=( ξP : A/K ).s. Cette substitution
appartient à l'ensemble
[[ ξ : K,Ψ;P : A,Γ]]Φ ;Γ .
-
- Preuve.
Nous remarquons tout d'abord que Φ ;Γ ⊢
t ▷ ξ : K,Ψ;P : A,Γ. Nous devons alors
montrer que ∀ (x : B)∈ξ : K,Ψ;P :
A,Γ, x [ t ] ∈[[ B]]Φ ;Γ . Soit un tel (x : B).
Nous remarquons que le terme x [ t ] est un terme neutre.
Nous en déduisons, par le
point 4 du
lemme 63, que pour montrer
l'appartenance de x [ t ] à [[ B]]Φ ;Γ , il nous suffit
de montrer l'appartenance de tous ses réduits en un pas à cet
ensemble. Nous déduisons du point 1
du lemme 66 que s est fortement
normalisable. Nous raisonnons alors par récurrence sur
ν(s) et par cas sur le réduit possible de x [ t ] .
-
Si x [ ( ξP : A/K ).s ] x [ ( ξP : A/K ).s' ] avec s→ s',
nous obtenons le résultat par hypothèse d'induction.
- Si x [ ( ξP : A/K ).s ] x [ s ] , nous obtenons le résultat du l'appartenance de s
à [[ Ψ;Δ]]Φ ;Γ .
Lemme 73
Soient deux termes M et N. Si M et N sont respectivement
dans [[ A]]Φ ;Γ et [[ B]]Φ ;Γ et si x est une variable
usuelle fraîche alors:
-
Le terme
UA''=def (λ _ :
B. x) [ ( x/M ).id ] N, où x est une variable
usuelle fraîche, appartient à [[ A]]Φ ;Γ et le terme
UB''=def (λ x : B. x) [ id ] N
appartient à [[ B]]Φ ;Γ .
- Le terme
UA'=def ( (λ x : A. λ _ :
B. x) [ id ] M) N appartient à [[ A]]Φ ;Γ et
le terme UB'=def ( (λ _ :
A. λ x : B. x) [ id ] M) N appartient à
[[ B]]Φ ;Γ .
- Le terme
⟨ M, N ⟩ appartient à [[ A× B]]Φ ;Γ .
-
- Preuve.
Nous remarquons tout d'abord que par le
point 1 du
lemme 63, M et N sont fortement
normalisables. Nous allons alors montrer ces trois assertions par
récurrence sur Σ=ν(M)+ν(N).
-
Nous ne montrons ici que l'appartenance de UA'' à
[[ A]]Φ ;Γ , la démonstration de la seconde appartenance
étant similaire. Nous remarquons que le terme UA'' est un
terme neutre et donc par le
point 4 du
lemme 63, il nous suffit, pour
obtenir le résultat, de montrer que tous les réduits en un pas de
UA'' sont dans [[ A]]Φ ;Γ . Or le terme UA'' ne peut se
réduire en un pas que vers:
-
(λ _ :
B. x) [ ( x/M' ).id ] N où M→ M' et dans ce
cas nous concluons par hypothèse d'induction.
- (λ _ :
B. x) [ ( x/M ).id ] N' où N→ N' et dans ce
cas nous concluons par hypothèse d'induction.
- x [ ( x/M ).id ] qui appartient bien à
[[ A]]Φ ;Γ . En effet, nous savons que M∈[[ A]]Φ ;Γ
par hypothèse. De plus par le
corollaire 68 nous savons de plus que
id∈[[ Φ ;Γ ]]Φ ;Γ . Donc, par le
lemme 70, nous
obtenons ( x/M ).s∈[[ Φ;x :
A,Γ]]Φ ;Γ . Et donc par définition des substitutions
réductibles (définition 62) nous avons
bien x [ ( x/M ).s ] ∈[[ A]]Φ ;Γ .
- Nous ne montrons ici que l'appartenance de UA' à
[[ A]]Φ ;Γ , la démonstration de la seconde appartenance
étant similaire. Nous remarquons que le terme UA' est un
terme neutre et donc par le
point 4 du
lemme 63, il nous suffit, pour
obtenir le résultat, de montrer que tous les réduits en un pas de
UA' sont dans [[ A]]Φ ;Γ . Or le terme UA' ne peut se
réduire en un pas que vers:
-
( (λ x : A. λ _ :
B. x) [ id ] M') N où M→ M' et dans ce cas
nous concluons par hypothèse d'induction.
- ( (λ x : A. λ _ :
B. x) [ id ] M) N' où N→ N' et dans ce cas
nous concluons par hypothèse d'induction.
- UA'' et dans ce cas nous concluons par le
point 1.
- Nous devons montrer que PA× B1(⟨ M, N ⟩) et
PA× B2(⟨ M, N ⟩) appartiennent respectivement à
[[ A]]Φ ;Γ et [[ B]]Φ ;Γ . Nous ne montrons ici que
l'appartenance de PA× B1(⟨ M, N ⟩) à
[[ A]]Φ ;Γ , la seconde appartenance étant similaire. Nous
remarquons que le terme PA× B1(⟨ M, N ⟩) est un
terme neutre et donc par le
point 4 du
lemme 63, il nous suffit, pour
obtenir le résultat, de montrer que tous les réduits en un pas de
ce terme sont dans [[ A]]Φ ;Γ . Or ce terme ne peut se
réduire en un pas que vers:
-
PA× B1(⟨ M', N ⟩) où M→ M' et dans ce
cas nous obtenons le résultat par hypothèse d'induction.
- PA× B1(⟨ M, N' ⟩) où N→ N' et dans ce
cas nous obtenons le résultat par hypothèse d'induction.
- UA' et nous concluons grâce au
point 2.
Lemme 74
Si M et N sont deux termes et s est un une substitution tels
que M [ s ] et N [ s ] soient respectivement dans
[[ A]]Φ ;Γ et [[ B]]Φ ;Γ alors ⟨ M, N ⟩ [ s ]
est dans T=[[ A× B]]Φ ;Γ .
-
- Preuve.
Il est évident que Φ ;Γ ⊢ T : A× B. Nous devons donc
montrer que PA× B1(T) et PA× B2(T) sont
respectivement dans [[ A]]Φ ;Γ et [[ B]]Φ ;Γ . Nous ne
montrons ici que la première appartenance la démonstration de la
seconde appartenance étant similaire. Nous allons raisonner par
récurrence sur Σ=ν( M [ s ] ) +
ν( N [ s ] ). Nous remarquons que le terme
PA× B1( ⟨ M, N ⟩ [ s ] ) est un terme neutre et
donc par le point 4 du
lemme 63, il nous suffit, pour
obtenir le résultat, de montrer que tous les réduits en un pas de
ce terme sont dans [[ A]]Φ ;Γ . Or ce terme ne peut se réduire
en un pas que vers:
-
PA× B1( ⟨ M', N ⟩ [ s ] ) où M→ M' et
dans ce cas nous obtenons le résultat par hypothèse d'induction.
- PA× B1( ⟨ M, N' ⟩ [ s' ] ) où N→ N'
et dans ce cas nous obtenons le résultat par hypothèse d'induction.
- PA× B1( ⟨ M, N ⟩ [ s' ] ) où s→ s' et
dans ce cas nous obtenons le résultat par hypothèse d'induction.
- PA× B1(⟨ M [ s ] , N [ s ] ⟩) qui
appartient bien à [[ A]]Φ ;Γ . En effet nous savons par
hypothèse que M [ s ] et N [ s ] appartiennent
respectivement à [[ A]]Φ ;Γ et [[ B]]Φ ;Γ et donc par
le point 3 du
lemme 73, nous déduisons
que ⟨ M [ s ] , N [ s ] ⟩. Nous concluons alors
grâce à la définition 62.
Lemme 75
-
Soient un
terme M appartenant à [[ A]]Φ;P :
B,Γ, un terme N appartenant à
[[ A]]Φ;Q : C,Γ et ξ une
variable de choix fraîche. Si Φ;[ξ ∣ P,Q ] : B+
C,Γ est compatible et linéaire alors U=[ξ ∣ M,N ]
appartient à l'ensemble [[ A]]Φ;[ξ ∣ P,Q ] : B+
C,Γ.
- Si M
et N sont deux termes appartenant à
[[ A]]Φ;Γ et si ξ est une
variable appartenant à Φ alors U=[ξ ∣ M,N ] appartient
à l'ensemble [[ A]]Φ;Γ.
-
- Preuve.
Nous commençons par remarquer que dans les deux cas, U est un
terme bien typé et neutre. De plus, par le
point 1 du
lemme 63, nous savons que dans les
deux cas M et N sont tous deux fortement normalisables et donc
que nous allons pouvoir raisonner par récurrence sur
Σ=ν(M) + ν(N). Par le
point 4 du
lemme 63, il nous suffit de montrer
que tous les réduits en un pas de U sont réductibles. Nous
poursuivons notre analyse en étudiant les différents réduits
possibles en un pas. Les réduits en un pas de [ξ ∣ M,N ]
sont:
-
[ξ ∣ M',N ] où M→ M' et nous concluons par hypothèse d'induction.
- [ξ ∣ M,N' ] où N→ N' et nous concluons par hypothèse d'induction.
Lemme 76
Soit Ξ un terme de choix fortement normalisable.
-
Si
le terme M [ s ] appartient à
[[ A]]Φ;P : B,Γ, et si le terme
N [ s ] appartient à [[ A]]Φ;Q :
C,Γ, ξ est une variable de choix fraîche,
Φ ;Γ ⊢Ξ ↝ ξ et si
Φ;[ξ ∣ P,Q ] : B+ C,Γ est compatible et
linéaire alors le terme U=[Ξ ∣ s M,N ] est dans
l'ensemble [[ A]]Φ;[ξ ∣ P,Q ] : B+
C,Γ.
- Si
les deux termes M [ s ] et N [ s ] appartiennent à
l'ensemble [[ A]]Φ ;Γ et si Φ ;Γ ⊢Ξ ↝ K
alors U=[Ξ ∣ s M,N ] est dans l'ensemble
[[ A]]Φ ;Γ .
-
- Preuve.
Nous remarquons que, dans les deux cas, le terme U est neutre.
Donc dans les deux cas, par le
lemme 63
(point 4), il nous suffit de
montrer que tous les réduits de U en un pas sont réductibles.
Puisque M [ s ] et N [ s ] sont tous les deux
fortement normalisables (par le
point 1 du
lemme 63), nous allons pouvoir
raisonner par récurrence sur la somme Σ=ν(M) + ν(N)+ ν(s) + ν(Ξ) puis par cas sur les réduits
possibles de U.
-
Dans ce cas, les différents réduits de U sont:
-
[Ξ' ∣ s M,N ] où
ΞΞ' et dans ce cas nous concluons par hypothèse d'induction
puisque le théorème 56, nous
garanti que Φ ;Γ ⊢Ξ' ↝ ξ.
- [Ξ ∣ s M',N ] où M→ M' et dans ce cas
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que M' [ s ] est réductible.
- [Ξ ∣ s M,N' ] où N→ N' et, dans ce cas,
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que N' [ s ] est réductible.
- [Ξ ∣ s' M,N ] où s→ s' et, dans ce cas,
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que M [ s ] et N' [ s ] sont réductibles.
- Ξ=ξ, [ξ ∣ M [ s ] , N [ s ] ]
qui appartient bien à [[ A]]Φ;[ξ ∣ P,Q ] :
B+C,Γ. En effet, nous savons que M [ s ] et
N [ s ] sont respectivement dans les ensembles
[[ A]]Φ;P : B,Γ et
[[ A]]Φ;Q : C,Γ et donc nous
pouvons conclure par le
point 1 du
lemme 75.
- Dans ce cas, les différents réduits de U sont:
-
[Ξ' ∣ s M,N ] où
ΞΞ' et dans ce cas nous concluons par hypothèse d'induction
puisque le théorème 56 nous
garantit que Φ ;Γ ⊢Ξ' ↝ K.
- [Ξ ∣ s M',N ] où M→ M' et, dans ce cas,
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que M' [ s ] est réductible.
- [Ξ ∣ s M,N' ] où N→ N' et, dans ce cas,
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que N' [ s ] est réductible.
- [Ξ ∣ s' M,N ] où s→ s' et, dans ce cas,
nous concluons par hypothèse d'induction puisque le
lemme 63
(point 3) nous garantit
que M [ s ] et N' [ s ] sont réductibles.
- Ξ=ξ, [ξ ∣ M [ s ] , N [ s ] ]
qui appartient bien à [[ A]]Φ;[ξ ∣ P,Q ] :
B+C,Γ. En effet, nous savons que M [ s ] et
N [ s ] sont respectivement dans les ensembles
[[ A]]Φ;P : B,Γ et
[[ A]]Φ;Q : C,Γ et donc nous
pouvons conclure par le
point 2 du
lemme 75.
- Ξ = L, M [ s ] et nous concluons par
hypothèse.
- Ξ = R, N [ s ] et nous concluons par
hypothèse.
Lemme 77
-
Soient s une substitution et M et N deux termes. Supposons
que s vérifie Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ s
▷ ΦΦ';[ξ ∣ P,Q ] : B+C,ΓΓ' et que
M [ s ] et N [ s ] soient respectivement dans
[[ A]]Φ;P : B,Γ et
[[ A]]Φ;Q : C,Γ. Si ξ est
une variable de choix fraîche et si
ΦΦ';ΓΓ'⊢ξ ↝ ξ alors
le terme U= [ξ ∣ M,N ] [ s ] appartient à l'ensemble
[[ A]]Φ;[ξ ∣ P,Q ] : B+C,Γ.
-
Soient s une substitution et M et N deux termes. Supposons
que s vérifie Φ;Γ⊢ s ▷
ΦΦ';ΓΓ' et que M [ s ] et
N [ s ] soient tous les deux dans
[[ A]]Φ;Γ. Si ξ est une
variable de choix telle que
ΦΦ';ΓΓ'⊢ξ ↝ K alors le
terme U= [ξ ∣ M,N ] [ s ] appartient à l'ensemble
[[ A]]Φ;Γ.
-
- Preuve.
Nous remarquons que, dans les deux cas, le terme U est neutre.
Donc dans les deux cas, par le
lemme 63
(point 4), il nous suffit de
montrer que tous les réduits de U en un pas sont réductibles.
Puisque M [ s ] et N [ s ] sont tous les deux
fortement normalisables (par le
point 1 du
lemme 63), nous allons pouvoir
raisonner par récurrence sur la somme Σ = ν(M) +
ν(N) + ν(s) puis par cas sur les réduits possibles de
U. Dans les deux cas, nous raisonnons comme suit:
-
Si U→ [ξ ∣ M',N ] [ s ] où M→ M', nous
obtenons le résultat par hypothèse d'induction.
- Si U→ [ξ ∣ M,N' ] [ s ] où N→ N', nous
obtenons le résultat par hypothèse d'induction.
- Si U→ [ξ ∣ M,N ] [ s' ] où s→ t', nous
obtenons le résultat par hypothèse d'induction.
- Si U[ ξ [ s ] ∣ s M,N ], par le
lemme 69, nous
savons que ξ [ s ] est fortement normalisable et
nous concluons grâce au
lemme 76.
Lemme 78
-
Soient s et t deux substitutions, M et N deux termes et
Ξ un terme de choix. Supposons que s vérifie
Φ;[ξ ∣ P,Q ] : B+C,Γ⊢ s ▷
ΦΦ';[ξ ∣ P,Q ] : B+C,ΓΓ', que
M [ t ∘ s ] et N [ t ∘ s ] soient
respectivement dans [[ A]]Φ;P : B,Γ
et [[ A]]Φ;Q : C,Γ, et que
Ξ soit fortement normalisable. Si ξ est une
variable de choix fraîche et si
ΦΦ';ΓΓ'⊢Ξ ↝ ξ alors
le terme U= [Ξ ∣ t M,N ] [ s ] appartient à
l'ensemble [[ A]]Φ;[ξ ∣ P,Q ] : B+C,Γ.
-
Soient s et t deux substitutions, M et N deux termes et
Ξ un terme de choix. Supposons que s vérifie
Φ;Γ⊢ s ▷
ΦΦ';ΓΓ', que M [ t ∘ s ]
et N [ t ∘ s ] soient tous les deux dans
[[ A]]Φ;Γ et que Ξ soit
fortement normalisable. Si ξ est une variable de choix
telle que ΦΦ';ΓΓ'⊢Ξ ↝ K
alors le terme U= [Ξ ∣ t M,N ] [ s ] appartient
à l'ensemble [[ A]]Φ;Γ.
-
- Preuve.
Nous remarquons que, dans les deux cas, le terme U est neutre.
Donc dans les deux cas, par le
lemme 63
(point 4), il nous suffit de
montrer que tous les réduits de U en un pas sont réductibles.
Puisque M [ t ∘ s ] et N [ t ∘ s ]
sont tous les deux fortement normalisables (par le
point 1 du
lemme 63), nous allons pouvoir
raisonner par récurrence sur la somme Σ = ν(M) +
ν(N) + ν(s) + ν(t) puis par cas sur les réduits
possibles de U. Dans les deux cas, nous raisonnons comme suit:
-
Si U→ [Ξ ∣ t M',N ] [ s ] où M→ M',
nous obtenons le résultat par hypothèse d'induction.
- Si U→ [Ξ ∣ t M,N' ] [ s ] où N→ N',
nous obtenons le résultat par hypothèse d'induction.
- Si U→ [Ξ ∣ t M,N ] [ s' ] où s→ s',
nous obtenons le résultat par hypothèse d'induction.
- Si U→ [Ξ ∣ t' M,N ] [ s ] où t→ t',
nous obtenons le résultat par hypothèse d'induction.
- Si U→ [Ξ' ∣ t M,N ] [ s ] où
ΞΞ', nous obtenons le résultat par hypothèse d'induction.
- Si Ξ=L et si U M [ t ] s [ ≡ ] M [ t ∘ s ] nous
concluons par hypothèse.
- Si Ξ=R et si U N [ t ] s [ ≡ ] N [ t ∘ s ] nous
concluons par hypothèse.
- Si Ξ=ξ et si U [ξ ∣ M [ t ] , N [ t ] ] [ s ] nous concluons
par le
lemme 77.
Lemme 79
Soient un terme M, deux types A et B et un environnement de
types linéaire et compatible Φ ;Γ . Si x, y, w1 et
w2 sont des variables usuelles fraîches, si ξ est une
variable de choix fraîche et si M appartient à l'ensemble
[[ A]]Φ ;Γ alors le terme inlB(M) est dans l'ensemble
[[ A+ B]]Φ;w1 : A, w2 : B,Γ.
-
- Preuve.
Nous allons en fait montrer les cinq points suivants:
-
La
substitution est telle que:
| t= ( ξy : B/L ).id∈[[ ξ : L,Φ;y : B,w1 : A,
w2 : B,Γ]]Φ;w1 : A, w2 :
B,Γ |
- nous en
déduirons que la substitution s=( x/M ).t appartient à
l'ensemble [[ ξ : L,Φ;x : A,y : B,w1 :
A, w2 : B,Γ]]Φ;w1 : A, w2 :
B,Γ.
- Et donc
le terme U''= [ξ ∣ ⟨ x, w2 ⟩,⟨ w1, y ⟩ ] [ s ]
est dans l'ensemble [[ A× B]]Φ;w1 : A, w2 :
B,Γ.
- D'où
U'= (λ x :
A. [ξ ∣ ⟨ x, w2 ⟩,⟨ w1, y ⟩ ]) [ t ] M est
dans l'ensemble [[ A× B]]Φ;w1 : A, w2 :
B,Γ.
- Enfin,
nous montrerons que le terme inlB(M) est dans l'ensemble
[[ A+ B]]Φ;w1 : A, w2 : B,Γ.
Nous allons procéder dans l'ordre.
-
Par le lemme 72,
il suffit de montrer que id appartient à
[[ Φ;w1 : A, w2 : B,Γ]]Φ;w1 : A, w2 :
B,Γ ce qui est
évident par le corollaire 68.
- Par le lemme 70, il
suffit de montrer que M∈[[ A]]Φ;w1 : A,
w2 : B,Γ, ce qui est vrai par le
lemme 64, et que
t∈[[ ξ : L,Φ;y : B,w1 : A,
w2 : B,Γ]]Φ;w1 : A, w2 :
B,Γ ce que nous avons démontré au
point 1.
- Par le
point 2
du
lemme 77,
il nous suffit de montrer que
s∈[[ ξ : L,Φ;x : A,y : B,w1 :
A, w2 : B,Γ]]Φ;w1 : A, w2 :
B,Γ, ce que nous avons démontré au
point 2, et que
les deux termes ⟨ x, w2 ⟩ [ s ] et
⟨ w1, y ⟩ [ s ] sont réductibles. Nous ne démontrons
ici que la réductibilité de ⟨ x, w2 ⟩ [ s ] , l'autre
cas étant similaire. Par le
lemme 74, il
nous suffit de démontrer que x [ s ] et w2 [ s ]
sont réductibles. Or ces deux cas sont trivialement résolus par
la définition 62 puisque s est réductible.
- Nous remarquons que U' est un terme neutre et donc que, par
le point 4 du
lemme 63, il nous suffit de
montrer que tous les réduits en un pas de U' sont réductibles.
De plus puisque M est réductible, par le
point 1 du
lemme 63, nous pouvons raisonner
par récurrence sur ν(M) et par cas sur les différents
réduits de U' en un pas qui sont:
-
(λ x :
A. [ξ ∣ ⟨ x, w2 ⟩,⟨ w1, y ⟩ ]) [ t ] M' où
M→ M' et dans ce cas nous concluons par hypothèse d'induction.
- U'' et nous concluons par le
point 3.
- Puisque inlB(M) est de type A+B dans l'environnement
Φ ;Γ , nous devons montrer que SA+B(inlB(M))
est dans [[ A×
B]]Φ;w1 : A, w2 : B,Γ. Puisque SA+B(inlB(M)) est un terme neutre,
il nous suffit, par le
point 4 du
lemme 63, de montrer que tous ses
réduits en un pas sont réductibles. Par le
point 1 du
lemme 63, nous pouvons raisonner
par récurrence ν(M) et par cas sur les différents réduits
de SA+B(inlB(M)) qui sont:
-
SA+B(inlB(M')) où M→ M' et dans ce cas
nous concluons par hypothèse d'induction.
- U' et dans ce cas nous concluons par le
point 4.
Lemme 80
Soient un terme M, deux types A et B et un environnement de
type linéaire et compatible Φ ;Γ . Si x, y, w1 et w2
sont des variables usuelles fraîches, si ξ est une variable
de choix fraîche et si M appartient à l'ensemble [[ B]]Φ ;Γ
alors le terme inrA(M) est dans l'ensemble
[[ A+ B]]Φ;w1 : A, w2 : B,Γ.
-
- Preuve.
La preuve de ce lemme est similaire à celle du
lemme 79.
Lemme 81
Soient un terme M et une substitution s. Si le terme
M [ s ] est dans [[ A]]Φ ;Γ alors:
-
Le
terme inlB(M) [ s ] appartient à [[ A+B]]Φ ;Γ .
-
Le terme inrB(M) [ s ] appartient à [[ B+A]]Φ ;Γ .
-
- Preuve.
Nous ne montrons ici que la preuve du
point 1, la
démonstration de l'autre point étant similaire. Par la
définition 62, il nous faut montrer que
U= SA+B(inlB(s)) appartient à
[[ A× B]]Φ;w1 : A,w2 : B. Puisque U
est neutre, il nous suffit, par le
point 4 du
lemme 63, de montrer que tous les
réduits de U en un pas sont réductibles. Par le
point 1 du
lemme 63, nous pouvons raisonner par
récurrence sur ν(M) + ν(s) et par cas sur les
différents réduits de U qui sont:
-
SA+B( inlB(M') [ s ] ) où M→ M' et dans
ce cas nous concluons par hypothèse d'induction.
- SA+B( inlB(M) [ s' ] ) où s→ s' et dans
ce cas nous concluons par hypothèse d'induction.
- SA+B(inlB( M [ s ] )) qui est bien dans
[[ A× B]]Φ;w1 : A,w2 : B. En
effet, par hypothèse nous savons que
M [ s ] ∈[[ A]]Φ ;Γ , donc, par le
point 5 du
lemme 79, nous avons
inlB( M [ s ] )∈[[ A+B]]Φ ;Γ . Nous concluons alors
par la définition 62.
Enfin, nous pouvons projeter grâce au
point 3 du
lemme 63 et donc remarquer que:
Remarque 82
Si ⟨ N1, N2 ⟩ est réductible alors N1 et N2 sont
réductibles. Si inl (N) ou si inr (N) est réductible alors N
est réductible.
Nous allons maintenant démontrer le théorème principal de cette
section.
4.4.4 Préservation de la réductibilité par composition
Théorème 83
Soient Φ ;Γ et Φ ';Γ ' deux environnement de types
compatibles et linéaires et soit s une substitution appartenant à
[[ Φ ';Γ ']]Φ ;Γ .
-
Pour toute substitution t telle que
Φ ';Γ '⊢ t ▷ Φ '';Γ '', la substitution
t ∘ s appartient à [[ Φ '';Γ '']]Φ ;Γ .
- Pour tout terme M tel que Φ ';Γ '⊢ M :
A, le terme M [ s ] appartient à [[ A]]Φ ;Γ .
-
- Preuve.
Nous remarquons tout d'abord que le terme M [ s ] et la
substitution t ∘ s sont bien typés dans Φ ;Γ . De
même, par le corollaire 45, nous
pouvons supposer que Γ=Des(Γ). Nous allons maintenant
montrer ces deux propositions ensemble par induction sur les
structure de M et de s.
-
Si t=id, nous remarquons que id ∘ s est une
expression neutre. Ainsi par le
point 4 du
lemme 63, il nous suffit de
montrer que tout les réduits en un pas de id ∘ s sont
dans [[ Φ ';Γ ']]Φ ;Γ . De plus, s étant réductible,
nous allons pouvoir raisonner par récurrence sur ν(s).
Les réduits en un pas possibles de id ∘ s sont:
-
• id ∘ s' où s→ s' et nous obtenons
le résultat par hypothèse de récurrence.
- • s et nous obtenons le résultat par hypothèse.
- Si t=( x/N ).t' alors, par le
lemme 49, Γ''=x : B,Γ'''. Par hypothèse d'induction,
nous savons que N [ s ] ∈[[ A]]Φ ;Γ et que
t' ∘ s∈[[ Φ;Γ''']]Φ ;Γ . Nous
concluons alors grâce au
lemme 71.
- Si t=t1 ∘ t2, par le
lemme 49, il existe alors un environnement
de types Φ ''';Γ ''' tel que Φ ';Γ '⊢ t2 ▷
Φ ''';Γ ''' et Φ ''';Γ '''⊢ t1 ▷ Φ '';Γ ''. Nous
obtenons alors par hypothèse d'induction,
t2 ∘ s∈[[ Φ ''';Γ ''']]Φ ;Γ et donc, en
appliquant l'hypothèse d'induction à ce nouveau résultat
t1 ∘ (t2 ∘ s)≡t ∘ s∈[[ Φ '';Γ '']]Φ ;Γ .
- Si M=x alors puisque Φ ';Γ '⊢ x : A nous devons
avoir Γ=x : A,Γ''' et donc nous obtenons le résultat par
la définition 62.
- Si M= M1 M2 alors par hypothèse d'induction, nous savons que
M1 [ s ] ∈[[ B→A]]Φ ;Γ et
M2 [ s ] ∈[[ B]]Φ ;Γ . Donc par définition de la
réductibilité, nous savons que
M1 [ s ] M2 [ s ] ≡ ( M1 M2) [ s ] ∈[[ A]]Φ ;Γ .
- Si M=⟨ M1, M2 ⟩ alors A=A1× A2 et par hypothèse d'induction nous
obtenons M1 [ s ] et M2 [ s ] respectivement dans
[[ A1]]Φ ;Γ et [[ A2]]Φ ;Γ . Nous concluons alors
grâce au
lemme 74.
- Si A=A1+A2 et M=inlA2(M1) alors par hypothèse d'induction nous
obtenons M1 [ s ] ∈[[ A1]]Φ ;Γ . Nous concluons
alors grâce au
lemme 81.
- A=A1+A2 et M=inrA1(M1), nous raisonnons comme dans
le cas précédent.
- Si M=[ξ ∣ M1,M2 ], le résultat est obtenu par hypothèse d'induction et
par le
lemme 77.
- Si M=[Ξ ∣ t' M1,M2 ], le résultat est alors obtenu
par hypothèse d'induction et par le
lemme 78.
Nous remarquons que pour pouvoir appliquer le lemme
78,
nous devons montrer que Ξ est fortement normalisable ce
que nous démontrons comme suit:
-
• Si Ξ = ξ ou Ξ = K, il
est évident que Ξ est fortement normalisable.
- • Si Ξ = ξ [ t ] alors, par
hypothèse d'induction, t ∘ s est fortement normalisable et donc t est
fortement normalisable et donc finalement Ξ est
fortement normalisable.
- Si M= M1 [ t' ] , alors par hypothèse d'induction,
t' ∘ s∈[[ Φ '';Γ '']]Φ ;Γ et donc
M [ t' ] [ s ] =≡ M [ t' ∘ s ] est
bien réductible.
- Si A=A1→ A2 et M=λ P : A1. M1, nous devons
alors, par définition des termes réductibles
(définition 62), montrer que ∀
N∈[[ A1]]Φ;ΓΔ,
U= (λ P :
A1. M1) [ s ] N∈[[ A2]]Φ;ΓΔ.
Puisque U est un terme neutre, par le
point 4 du
lemme 63, il nous suffit de
montrer que tous ses réduits en un pas appartiennent à cet
ensemble. Commençons tout d'abord par remarquer que, par le
lemme 47, nous connaissons
une dérivation de Φ';P : A1,Γ'⊢ M1 :
A2 et, par le lemme 41, il existe une preuve
de Φ;P : A1,Γ⊢ s ▷
Φ';P : A1,Γ'. Nous obtenons alors par hypothèse d'induction,
M1 [ s ] ∈[[ A2]]Φ;P :
A1,Γ. Donc en particulier, par le
point 1 du
lemme 63, M1 et s sont
fortement normalisables. Nous allons donc raisonner par
induction sur l'ordre lexicographique induit par la structure de
P et par la somme Σ = ν(M) + ν(s). Nous
remarquons de plus que par le
lemme 67,
s∈[[ Φ';Γ'Δ]]Φ;ΓΔ.
Les différentes réductions en un pas de U sont:
-
• U (λ P :
A1. M1') [ s ] N où M1→ M1' et dans ce cas
nous obtenons le résultat par la seconde hypothèse d'induction.
- • U (λ P :
A1. M1) [ s' ] N où s→ s' et dans ce cas nous
obtenons le résultat par la seconde hypothèse d'induction.
- • U (λ P :
A1. M1) [ s ] N' où N→ N' et dans ce cas nous
obtenons le résultat par la seconde hypothèse d'induction.
- • Si P=⟨ P1, P2 ⟩, N=⟨ N1, N2 ⟩ et
U ( (λ P1. λ P2. M1) [ s ] N1) N2.
Mais, dans ce cas, par la
remarque 82,
nous savons que N1 et N2 sont réductibles. Par la seconde
hypothèse d'induction, nous en déduisons que
(λ P1. λ P2. M1) [ s ] N1 est
réductible et nous concluons par définition de termes
réductibles.
- • Si P=@(P1)P2 et
U ( (λ P1. λ P2. M1) [ s ] N) N,
nous raisonnons comme dans le cas précédent.
- • Si A1=C+D, P=[ξ ∣ P1,P2 ], N=inlD(N1)
et U (λ P1 :
C. M1) [ ( ξP2 : D/L ).s ] N1,
alors, par la
remarque 82,
nous savons que N1 est réductible. De plus, par le
lemme 72,
( ξP2 :
D/L ).s∈[[ ξ : L,Φ';P2 :
D, Γ'Δ]]Φ;ΓΔ. De même par le
lemme 52, nous savons que
ξ : L,Φ';P1 : C,P2 :
D,ΔΓ'⊢ M1 : A2. Donc par la seconde hypothèse d'induction,
nous obtenons, (λ P1 :
C. M1) [ ( ξP2 :
D/L ).s ] ∈[[ D→A2]]Φ;ΔΓ
et donc par définition des termes réductibles,
(λ P1 :
C. M1) [ ( ξP2 :
D/L ).s ] N1∈[[ A2]]Φ;ΔΓ.
- •Si A1=C+D, P=[ξ ∣ P1,P2 ], N=inrC(N1)
et U (λ P2 :
D. M1) [ ( ξP1 : C/R ).s ] N1,
nous raisonnons comme dans le cas précédent.
- • Si P=x et si
U M1 [ ( x/N ).s ] , alors par le
lemme 70 nous savons
que
( x/N ).s∈[[ Φ';x :
A,ΓΔ]]Φ;ΓΔ et donc, par la première hypothèse d'induction:
| M1 [ ( x/N ).s ] ∈[[ A2]]Φ;ΓΔ |
- •Si P= _ et si U M1 [ s ] , nous
raisonnons comme dans le cas précédent.
Nous sommes maintenant en mesure de démontrer la normalisation forte
de λ Pw/≡.
Théorème 84 (Normalisation forte
de λ Pw/≡) Toute expression bien typée du calcul λ Pw/≡ est fortement
normalisable.
-
- Preuve.
Soit e une expression bien typée du calcul λ Pw/≡. Si M est un
terme par le théorème 83 et le
corollaire 68, M [ id ] est
réductible. Et donc par le point 1
du lemme 63, M [ id ] est
fortement normalisable. Si e est une substitution, nous
raisonnons comme précédemment. Si e est un terme de choix,
plusieurs cas sont possibles:
-
Si e=ξ ou e=K, le résultat est évident.
- Si e= ξ [ s ] , alors par le
théorème 83 s ∘ id est
réductible. Donc par le point 1
du lemme 66, s ∘ id est
fortement normalisable. Nous en déduisons que s est elle-même
fortement normalisable. Nous concluons alors grâce au
lemme 69.
Nous en déduisons:
Théorème 85 (Normalisation forte
de λ Pw) Toute expression bien typée du calcul λ Pw est fortement
normalisable.
-
- Preuve.
Avant toute chose nous remarquons que nous pouvons considérer la
relation →λ Pw comme étant R1∪ R2 où R1 est la
relation induite par les règles définissant le λ Pw calcul
privées de (app), (ass_env) et (clos) et où R2
est induite par ces trois règles. Nous considérons alors O
l'ensemble de λ Pw-expressions, O' celui des
λ Pw/≡-expressions, T la congruence ≡ et R' la
relation →λ Pw/≡ . Nous concluons alors par le
lemme 8 et par le théorème 84
après avoir remarqué que R2 est fortement normalisante.